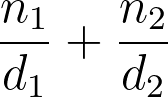Fraction Calculator

Welcome to our fraction calculator, a really versatile tool. It can:

• ➕ add;
• ➖ subtract;
• ✖️ multiply; and
• ➗ divide any two fractions.

Moreover, it has the ability to simplify a fraction (A.K.A. reduce), as well as tell you how to turn a fraction into a decimal, and vice versa. If you're still not impressed, this tool not only works on standard proper and improper fractions but also on mixed fractions – what more could you ask for? 😁

As usual, we've prepared some introductory reading, which will let you dig into the world of fractions 🌎. Below you'll read about the fraction definition, the types of fractions (proper, improper, mixed), and all those basic operations on simple and mixed fractions. Are you ready?

A fraction represents the number of equal parts of a whole thing.
You can recognize a simple fraction because it has two numbers separated by a line (or slash):

• We call the top number the numerator and write it above the line. It tells us:

  How many parts do we have.

• We call the bottom number denominator and display it below the line. It means:

  The total number of parts.

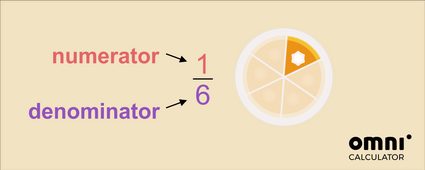
In the example above, it's one part out of six slices, which the pie was cut into in total. We read it as one-sixth of the whole pie.

But, of course, the cake can be cut differently!

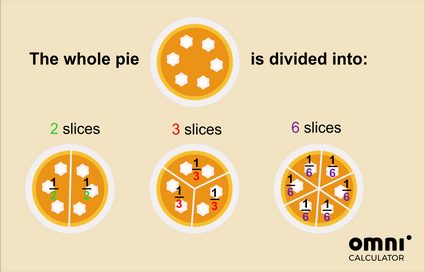
So, if you cut the pie in 2, then one slice is one-half of the whole. If you cut the pie in 3 parts, then one slice is one-third of the whole pie, etc.

Fractions are used all around us:

• Every time you want to express part of a whole item, which can be divided into even pieces: like a cake 🍰, a chocolate bar 🍫, a watermelon 🍉, a pizza 🍕, etc.;

• When we measure something 📏, especially in inches or eights of an inch; and

• Your computer screen size 🖥️ is expressed as a ratio, e.g., 16:9 – and it's also a fraction, just written in a different way. (For information on how to simplify ratios, check out our ratio calculator!)

So, now that you know the fraction definition, let's have a look at the different types of fractions. In general, we have three types of fractions: proper, improper, and mixed fractions:

1. Proper fractions

   In proper fractions, the top number (numerator) is smaller than the bottom number (denominator). It means that it will always be less than one whole thing, e.g.:

   🍰 5 slices of cake out of a cake that was cut into 6;

   🍫 2 rows of a chocolate bar out of the whole chocolate bar, which has 5 rows; and

   🍊 7 parts of an orange out of the entire orange that we cut into 8.

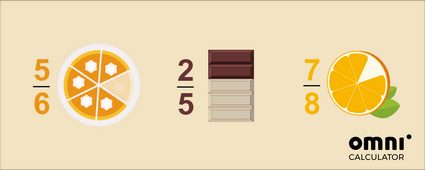
The general rule, which works for both positive and negative numbers, is that the absolute value of the fraction is less than one:

|^numerator/_denominator| < 1

2. Improper fractions

   So what is an improper fraction? It's a fraction where the numerator is larger than (or equal to) the denominator. Improper fractions are sometimes called top-heavy fractions. Examples of improper fractions are:

   🍰 10 slices of cake, when each cake has 6 slices;

   🍫 8 rows of a chocolate bar. A whole chocolate bar has 5 rows; and

   🍊 21 parts of orange, if we cut each orange into 8 equal pieces.

3. Mixed fractions

   Mixed fractions, also known as mixed numerals or mixed numbers, are another way of expressing an improper fraction. They are whole numbers (the number of whole things) and a proper fraction put together. So, we'll take a look at the examples from the previous paragraph:

   🍰 10 slices of cake, when each cake has 6 slices is the same as → 1 whole cake and 4 slices out of 6;

   🍫 8 rows of chocolate when the whole chocolate bar has 5 rows → 1 whole chocolate bar and 3 rows out of 5; and

   🍊 21 parts of orange, if we cut the orange to 8 slices → 2 whole oranges and five slices out of 8

When it comes to adding fractions, there are three scenarios:

1. The denominator (bottom number) is the same in both fractions – e.g., ³/₅ and ¹/₅

   This is the most straightforward case; all you need to do is to add numerators (top numbers) together and leave the denominator as is, e.g.:

   ➽ ³/₅ + ¹/₅ = ^{(3 + 1)}/₅ = ⁴/₅

2. The fractions have unlike denominators – e.g., ²/₅ and ³/₁₀

   This is a bit more of a complicated case – to add these fractions, you need to find the common denominator.

   • You can use, for example, LCM – the least common multiple to find the common number of your two denominators: LCM(5,10) = 10 Another option is to multiply your denominators and reduce the fraction later.

   • Then, you need to expand each fraction to have this common denominator as its bottom number:

   So, you should multiply the fraction with the denominator equal to 5 (our 1/5) by 2 to get 10 (remember that you must multiply both top and bottom numbers):

   ➽ ²/₅ = ^{(2 × 2)}/_{(5 × 2)} = ⁴/₁₀

   Your second fraction already has its denominator equal to 10:

   ➽ ³/₁₀

   • Now that your fractions have the same denominator, you can add them:

     ➽ ⁴/₁₀ + ³/₁₀ = ^{(4 + 3)}/₁₀ = ⁷/₁₀

3. You want to add two mixed fractions – e.g., 2 ³/₅ and 1 ¹/₂

   One solution for this kind of problem is to convert the mixed fraction to an improper fraction and sum it up as usual.

   Let's convert it for 2 ³/₅

   • Multiply the whole number by the denominator:

     2 × 5 = 10

   • Add the result to your numerator:

     10 + 3 = 13

   • That's your new numerator – write it on top of your denominator:

     2 ³/₅ = ¹³/₅

   Analogically, you can find out that 1 ¹/₂ = ³/₂.

   • Do the standard addition of fractions with uneven denominators:

     ➽ ¹³/₅ + ³/₂ = ²⁶/₁₀ + ¹⁵/₁₀ = ⁴¹/₁₀

   • Finally, you can convert your result back into a mixed fraction:

     Do long division with a remainder:

     ➽ ⁴¹/₁₀ = 4 R 1 = 4 ¹/₁₀

Of course, our fraction calculator deals with all of these scenarios. 😎

If you're still wondering how adding fractions works, maybe this visual will help?

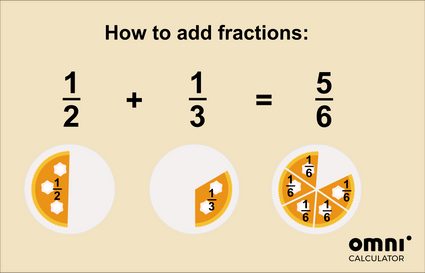
For an even more thorough explanation, check out our adding fractions calculator.

If you're wondering how to subtract fractions, and you've read through the previous section How do you add fractions, we have some good news for you: it's pretty much the same!

1. If you have fractions with the same denominator, subtract the numerators:

   ➽ ³/₅ - ¹/₅ = ^{(3 - 1)}/₅ = ²/₅

2. When subtracting fractions with unlike denominators – ²/₅ and ³/₁₀ – repeat the procedure from the previous section, but subtracting, not adding in the final step:

   • Find a common denominator – it's 10.

   • Expand the fractions to their equivalent fractions with a common denominator: ⁴/₁₀ and ³/₁₀.

   • Subtract the numerators.

     ➽ ²/₅ - ³/₁₀ = ⁴/₁₀ - ³/₁₀ = ¹/₁₀

3. For mixed fractions (2³/₅ and 1 ¹/₂):

   • Change the mixed fractions to improper fractions, as before:

     2 ³/₅ = ¹³/₅ and 1 ¹/₂ = ³/₂

   • Subtract the two improper fractions with unequal denominators:

     ➽ ¹³/₅ - ³/₂ = ²⁶/₁₀ - ¹⁵/₁₀ = ¹¹/₁₀

   • Leave it in an improper fraction, or convert it back to a mixed fraction:

     ➽ ¹¹/₁₀ = 1 R 1 = 1 ¹/₁₀

You can imagine subtraction as taking or eating part of the cake:

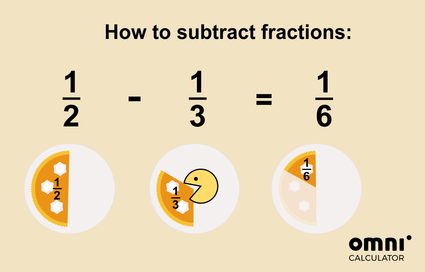
That wasn't so hard, was it?

Multiplying fractions is – fortunately – an effortless operation. It's numerator times numerator over denominator times denominator. Sometimes you also need to simplify the fraction. And that's it!

Take a look at this example:

➽ ²/₃ × ⁵/₆ = ^{(2 × 5)}/_{(3 × 6)} = ¹⁰/₁₈

which you can then simplify to ⁵/₉

Whenever you deal with mixed fractions, don't forget than you must always write them as an improper number before multiplying:

➽ 2 ¹/₂ × 3 ¹/₄ = ⁵/₂ × ¹³/₄ = ^{(5 × 13)}/_{(2 × 4)} = ⁶⁵/₈ = 8 ¹/₈

And when multiplying a fraction by a whole number, remember that you can write the whole number as itself divided by 1:

➽ 3 × ⁵/₇ = ³/₁ × ⁵/₇ = ^{(3 × 5)}/_{(1 × 7)} = ¹⁵/₇

If you don't know how to deal with fraction reduction, scroll down to the section How to simplify fractions.

Now that you know how do you multiply fractions, let's proceed to the next topic, fraction division.

Racking your brain over how to divide fractions? Have no worries! The division of fractions is quite similar to fraction multiplication. The only difference is that you must multiply your first number by the reciprocal of the second fraction. It may sound a bit weird, but it's really simple! Have a look at this example:

(¹/₂) / (³/₅) = ¹/₂ × ⁵/₃ = ^{(1 × 5)}/_{(2 × 3)} = ⁵/₆

So, all you need to do is turn the second fraction upside down (which is its reciprocal) and multiply the fractions. Sometimes, you may also need to do some fraction reduction. And that's all, tadaaa! 🎉

We always like to make our lives simpler – even in maths. That's why simplifying fractions is such an important thing. It means that we write the fraction in its simplest possible form. We also call simplifying fractions reducing fractions.

But what does this mean, exactly? Have a look at these examples:

• You'd rather say that one-fourth (a quarter) of the pizza is left, instead of two-eights, right?
• or half of a cake was eaten, not three-sixths

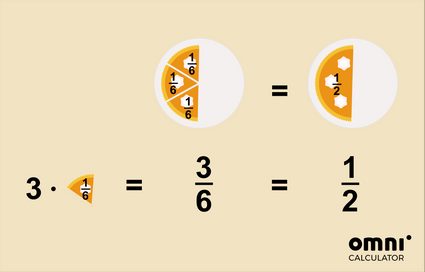
To simplify a fraction, you can use two methods:

1. Use a kind of brute force approach: divide the fraction by 2, 3, 5, 7, 11... until it's impossible to continue the division (without a remainder):

   ➽ ⁴²/₁₂₆ = /:2

   ➽ ²¹/₆₃ = /:3

   ➽ ⁷/₂₁ = /:7

   ➽ ¹/₃

2. Find the GCF – greatest common factor of the numerator and denominator, and then divide them by this number: GCF(42,126) = 42, so

   ➽ ⁴²/₁₂₆ = /:42

   ➽ ¹/₃

Read more about reducing fractions in our dedicated simplify fractions calculator. Also, make sure to have a look at our amazing equivalent fractions calculator, which can find many equivalents to your fraction.

If you want to find out how to convert a decimal into a fraction, you're in the right place. Here's a step-by-step guide:

Let's assume you want to convert 0.32 to a fraction:

1. Treat your decimal as a numerator. Then, the denominator will be 1.

2. Move the decimal dot to the right, till you only have a whole number:

   0.32 → 3.2 → 32

   Each move corresponds to multiplication by 10

   0.32 × 10 → 3.2 × 10 → 32

3. You multiplied the numerator by 10 × 10, and now we need to multiply the denominator by the same number:

   1 × 10 × 10 = 100

4. You've changed your fraction to a decimal! ✨ 0.32 → ³²/₁₀₀

5. Finally, simplify the result. As the greatest common factor for 32 and 100 is 4, divide both the numerator and denominator by this value:

   ➽ ³²/₁₀₀ = ⁸/₂₅

And that's it, the fraction in its simplest form. ❤️

Well, the easiest way to turn a fraction into a decimal is... to use a calculator. Be it this fraction calculator, a standard pocket calculator, or our dedicated tool – the fraction to decimal converter.

Sometimes the fraction is relatively easy to change into decimal without any tools – like for 1/2, 3/4 (or even 1/8). We believe that you can figure out how to expand the above fractions to have 10, 100, 1000, and so on in the denominator, respectively:

• Multiply ¹/₂ by 5 to get 10 as the denominator:

  ➽ ¹/₂ = ⁵/₁₀ = 0.5

• Multiply ³/₄ by 25 to get 100 as the denominator:

  ➽ ³/₄ = ⁷⁵/₁₀₀ = 0.75

• Multiply ¹/₈ by 125 to get 1000 as the denominator:

  ➽ ¹/₈ = ¹²⁵/₁₀₀₀ = 0.125

But what if you don't have the Internet or a calculator with you, but only pen and paper📝? And your fraction doesn't look so easy to expand as the ones above? Then, you'll probably need to do the long division to the decimal places by hand. Good luck! 🤞

You need to find a common denominator before you can. We will use 1/2 and 3/5 as an example. Follow these steps to add fractions with different denominators:

1. Find the least common multiple (LCM) of the denominator:

   10

2. Divide the LCM by each denominator and multiply the numerators by the answer:

   • 10/2 = 5
     5 × 1 = 5

   • 10/5 = 2
     2 × 3 = 6

3. Add the numbers found in Step 2 and place the answer over the LCM:

   • 6 + 5 = 11

   • 11/10 = 1 ¹/₁₀

4. Voila! You have added your fractions.

Yes, every fraction is a rational number, but not all rational numbers are fractions. A rational number is a fraction only when the numerator and denominator are whole numbers.

0.3333 written as a fraction is ³³³³/₁₀₀₀₀.

To find this answer:

1. Write the decimal as the numerator and 1 as the denominator:

   0.3333/1

2. Move the decimal point to the right at the end of the number so it appears as an integer:

   3333

3. Add the same number of zeros to the denominator as the number of places you moved the decimal point. In this instance, it is four:

   10000

4. Place the number from Step 2 as the numerator and the number in Step 3 as the denominator:

   3333/10000

The product of 1/2 and 5/3 is 5/6.

To arrive at this answer, we multiply the numerators and denominators in the following steps:

• 1 × 5 = 5; and

• 2 × 3 is 6; so

• 1/2 × 5/3 = 5/6