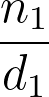Equivalent Fractions Calculator
Table of contents
What is an equivalent fraction?How to find equivalent fractions?How to use equivalent fractions calculator?What are equivalent fractions of…FAQsThis equivalent fractions calculator is a great tool that helps you find equivalent fractions for any fraction you wish. This is the right place to learn what is an equivalent fraction of x, or how to find equivalent fractions.
Wondering whether two fractions are equivalent? You can get the answer to this question as well!
🔎 If you want to go one step further and learn how to add fractions, check our adding fractions calculator!
Let's recall that a fraction is a ratio of two numbers, the numerator, A and the denominator, B. As you already know from the ratio calculator, the ratio is equal to some specific value, x, where x = A/B. But what does it mean that two fractions are equivalent?
What is an equivalent fraction?
The equivalent fraction definition tells us that any two fractions, A/B and C/D, are equivalent if they are equal to the same value. We can find whether two fractions are equivalent by checking one of these conditions:
A = CandB = D;A × D = B × C;C = k × AandD = k × B, for any numberk.
Converting two equivalent fractions to percentages will give us exactly the same number.
How to find equivalent fractions?
For any fraction, there are infinitely many equivalent fractions. It's convenient to present such values as a ratio of two integer numbers. That's how we divide things in everyday life, e.g., cutting a pizza into pieces (and taking a few of them).
As an example, let's check how to find equivalent fractions of 4/6. We can follow these steps:
-
Make sure both the numerator and denominator are integers. If not, start multiplying both numbers by 10 until there are no more decimal digits. In our case, both 4 and 6 are already integers.
-
Let's find the fraction in its simplest form. To do so, evaluate the greatest common factor of the numerator and the denominator. Here, the GCF of 4 and 6 is 2, so 4/6 is an equivalent fraction of 2/3, and the latter is the simplest form of this ratio. Therefore, 2/3 is our base.
🔎 For a more complex computation, feel free to use Omni's GCF calculator.
-
Multiply the base by consecutive natural numbers:
→ 2×2/2×3 = 4/6;
→ 3×2/3×3 = 6/9;
→ 4×2/4×3 = 8/12;
→ etc… -
All of the values are equivalent fractions of 2/3 and are also equivalent to 4/6, the number we started with.
The procedure is straightforward, but what if you want to find 20 or 30 equivalent fractions? Well, it gets pretty time-consuming. However, if you use our equivalent fractions calculator, we can save you all of that hassle.
You can always convert any decimal to a fraction and then work out what are its equivalent fractions from there.
How to use equivalent fractions calculator?
There are two different modes you can choose from. The first one helps you find as many fractions that are equivalent to your number as you want. Check the previous section for how these calculations work.
The second option helps you find if two fractions are equivalent. For instance, is 13/16 an equivalent fraction to 3/4? Let's check one of the conditions, e.g. multiply the numerator and denominator from the opposing fractions:
13 × 4 = 52;16 × 3 = 48.
The outcomes are different, so the fractions 13/16 and 3/4 are NOT equivalent. What about 12/16 and 3/4?
12 × 4 = 48;16 × 3 = 48.
This time, both numbers are the same, so 12/16 IS equivalent to 3/4. By using this equivalent fraction calculator, you can also see how to obtain one fraction from another!
What are equivalent fractions of…
Here is a list of a few fractions and their equivalent fractions:
-
Equivalent fractions of 1/1: 2/2, 3/3, 4/4, 5/5.
-
Equivalent fractions of 1/2: 2/4, 3/6, 4/8, 5/10.
-
Equivalent fractions of 1/3: 2/6, 3/9, 4/12, 5/15.
-
Equivalent fractions of 2/3: 4/6, 6/9, 8/12, 10/15.
-
Equivalent fractions of 1/4: 2/8, 3/12, 4/16, 5/20.
-
Equivalent fractions of 3/4: 6/8, 9/12, 12/16, 15/20.
-
Equivalent fractions of 1/5: 2/10, 3/15, 4/20, 5/25.
-
Equivalent fractions of 2/5: 4/10, 6/15, 8/20, 10/25.
-
Equivalent fractions of 3/5: 6/10, 9/15, 12/20, 15/25.
-
Equivalent fractions of 4/5: 8/10, 12/15, 16/20, 20/25.
-
Equivalent fractions of 1/6: 2/12, 3/18, 4/24, 5/30.
-
Equivalent fractions of 5/6: 10/12, 15/18, 20/24, 25/30.
How do I check if two fractions are equivalent?
To verify that two fractions are equivalent, simplify each of them by dividing its numerator and denominator by their greatest common factor. If at the end you get the same fraction for each, your initial fractions are equivalent. Otherwise, they are not equivalent.
How many equivalent fractions are there?
For each fraction, there is an infinite number of fractions that are equivalent to it. To see that, assume our fraction is a/b. Then the fraction k×a/k×b is equivalent to it for k equal to any number. So we see that there are indeed an infinite number of fractions that are equivalent to a given fraction.
How do I generate equivalent fractions?
To generate fractions equivalent to some given fraction:
- Write down your given fraction a/b.
- Write down the fractions 2a/2b, 3a/3b, etc.
- In general, write down fractions of the form k×a/k×b, where k is any number. To keep it simple, use integers.
- In this way, you can generate as many fractions equivalent to a/b as you wish!
Are 6/8 and 9/12 equivalent fractions?
Yes, 6/8 and 9/12 are equivalent. To see it, we simplify each of them:
- First, 6/8 = 3/4, when we divided the numerator and denominator by 2.
- Second, 9/12 = 3/4, when we divided the numerator and denominator by 3.
Since we arrived at the same result 3/4 twice, our initial fractions are indeed equivalent.
