Last updated: Apr 11, 2024

Foci of an Ellipse Calculator

Q: How many foci does an ellipse have?

An ellipse has a maximum of 2 foci. On the other hand, we can draw multiple numbers of ellipses on any two specified foci. We can also have an ellipse with only one focus. In that particular case, we form a circle - which is a special type of ellipse. Read more

Table of contents

What are the foci of an ellipse?How to find the foci of an ellipse How to use this foci of an ellipse calculator How to draw an ellipse using the foci of ellipse equation Other related calculators FAQs

This foci of an ellipse calculator will help you locate the foci of an ellipse, with respect to its center, given the values for its semi-major axis and the semi-minor axis. In this calculator, you will learn:

What foci of an ellipse are;
How to find the foci of an ellipse;
How to find the coordinates of the foci of an ellipse; and
How to draw an ellipse after finding the foci of an ellipse.

Keep on reading to start learning.

What are the foci of an ellipse?

An ellipse's foci, the plural of focus, are the two reference points of the locus of points that form the ellipse that we know. An ellipse's foci lie within the area of the ellipse along its principal axis - which is the axis that cuts through the longer dimension of the ellipse.

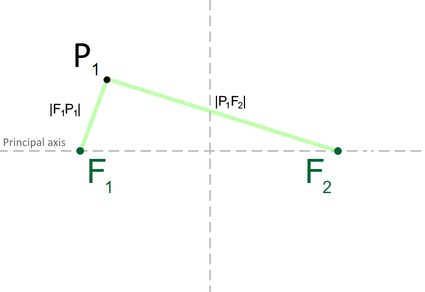
To better understand how the foci act as an ellipse's reference points, imagine drawing an arbitrary point, P₁, outside the principal axis and drawing two connecting lines |F₁P₁| (from the first focus, F₁, to P₁) and |P₁F₂| (from P₁ to the second focus, F₂), as shown in the image below:

Image showing two lines connecting the foci at point P1

Then, imagine drawing another pair of lines to another point, P₂, such that the total length of this new pair of lines, |F₁P₂| + |P₂F₂|, is equal to the total length of our first pair of lines |F₁P₁| + |P₁F₂|.

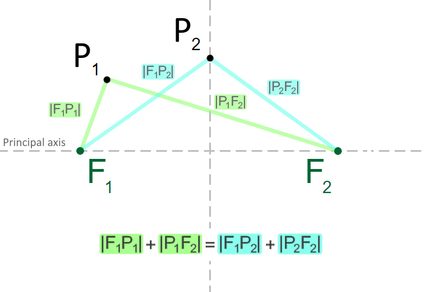
Illustration showing two sets of lines of equal total distances connecting the foci at two points P1 and P2.

If we continue this fashion to draw all the points P possible, we then form an ellipse, as shown in the illustration below:

Illustration of an ellipse formed by arbitrary points P.

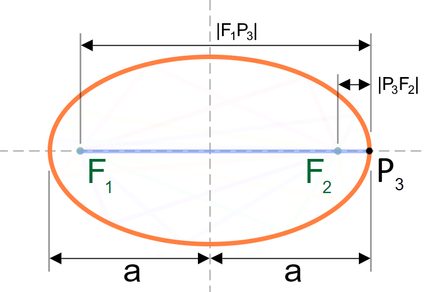
In the illustration above, by considering point P₃ along the principal axis, we can see that the total length of the pair of lines, |F₁P₃| + |P₃F₂|, equates to the major axis or the major diameter of our ellipse which is equal to a × 2, as we can better see illustrated below:

Illustration showing how |F₁P₃| + |P₃F₂| equates to a twice the semi-major axis, a.

On the other hand, by considering point P₂, which falls at the semi-minor axis at a distance b from the center, we form two right triangles. Since we already know that |F₁P₂| + |P₂F₂| is also equal to a × 2, we can say that |P₂F₂| = a, as shown in the illustration below:

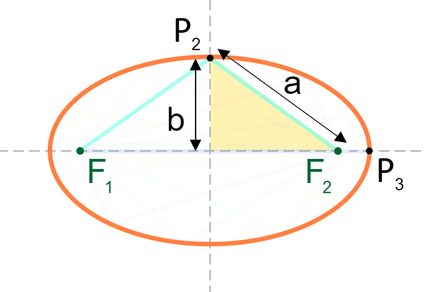
Illustration of an ellipse and right triangle formed by the axes and the line from a point on the ellipse.

With that in mind, we can go ahead and proceed to learn how to find the foci of an ellipse using the relationship between the distance to a focus from the ellipse's center, the semi-minor axis b, and semi-major axis a:

How to find the foci of an ellipse

From the image we got from the previous section of this text and based on the Pythagorean theorem, we can formulate the foci of an ellipse equation:

F = \sqrt{a^2-b^2}

where:

$F$ — Focal distance from an ellipse's center to one of its foci;
$a$ — Semi-major axis; and
$b$ — Semi-minor axis.

Using the focal distance, we can now determine the coordinates of the foci of an ellipse by following these notations:

For horizontal ellipses

$F_1 = (c_1-F,\ c_2)$
$F_2 = (c_1+F,\ c_2)$

For vertical ellipses

$F_1 = (c_1,\ c_2-F)$
$F_2 = (c_1,\ c_2+F)$

where:

$F_1$ & $F_2$ — Variables representing the foci of an ellipse;
$c_1$ — x-coordinate of the ellipse's center; and
$c_2$ — y-coordinate of the ellipse's center.

🙋 When the two foci of an ellipse intersect, we get a special type of ellipse we know as circle. That only happens when $a$ and $b$ are equal, and we calculate $F$ to be 0. We can also say that the circle's focus is on its center.

How to use this foci of an ellipse calculator

To use our foci of an ellipse calculator to find the coordinates of the foci of an ellipse:

First enter the coordinates of your ellipse's center.
Then, input the values for $a$ and $b$ of your ellipse.
You can also enter the coordinates of the vertices of your ellipse by clicking on the corresponding collapsed section at the bottom of our calculator.

Upon doing these steps, our foci of an ellipse calculator will then display the x and y coordinates of your ellipse's foci.

How to draw an ellipse using the foci of ellipse equation

We can use the knowledge we learned from our foci of an ellipse calculator to draw any size of an ellipse we want. But first, we have to calculate the foci of a sample ellipse. Let's say we want to draw an ellipse with a 3 cm semi-minor axis and a 5 cm semi-major axis. By substituting these measurements to our foci of an ellipse equation, we can obtain:

\scriptsize \begin{align*} F &= \sqrt{a^2-b^2}\\[.5em] &= \sqrt{(5\ \text{cm})^2-(3\ \text{cm})^2}\\[.5em] &= \sqrt{25\ \text{cm}^2-9\ \text{cm}^2}\\[.5em] &= \sqrt{16\ \text{cm}^2}\\[.5em] &= 4\ \text{cm} \end{align*}

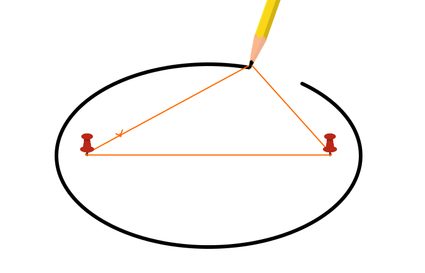
Now that we have our ellipse's focal distance, it's time to draw our ellipse. Here are the steps to follow:

Cut a string to make a loop with a perimeter equal to $2F + 2a$ or $2\times4\ \text{cm} + 2\times5\ \text{cm} = 18\ \text{cm}$ .
Push two pins on your drawing surface $2F$ or $2\times4\ \text{cm} = 8\ \text{cm}$ apart. The pins will represent our ellipse's foci.
Place the loop you made around the two pins and use a pencil to pull the loop taut.
Move the pencil around the pins while keeping the loop taut to draw our ellipse, as shown in the image below:

Image of drawing an ellipse using a loop of string and pins on the positions of the foci.

FAQs

How many foci does an ellipse have?

An ellipse has a maximum of 2 foci. On the other hand, we can draw multiple numbers of ellipses on any two specified foci. We can also have an ellipse with only one focus. In that particular case, we form a circle - which is a special type of ellipse.

How do I determine the foci of an ellipse?

To determine the foci on an ellipse with, let's say, 13 cm and 5 cm for their semi-major and semi-minor axes, respectively:

First, take the difference between the squares of the semi-major axis and the semi-minor axis: (13 cm)² - (5 cm)² = 144 cm².
Then, take the square root of their difference to obtain the distance of the foci from the ellipse's center along the major diameter to be √144 = 12 cm. This means that one focus lies 12 cm to the left of the ellipse's center, and one focus lies 12 cm to the right.

Ellipse with semiaxes, foci, center and vertices marked.

Ellipse parameters

(x − c₁)² / a² + (y − c₂)² / b² = 1

Center, x-coordinate (c₁)

Center, y-coordinate (c₂)

a

b

📌 First focus, F1

x-coordinate

y-coordinate

📌 Second focus F2

x-coordinate

y-coordinate

First vertex, V1

Second vertex, V2

First vertex, V3

Second vertex, V4

Check out 24 similar 2d geometry calculators 📏

AreaArea of a rectangleArea of crescent...21 more