Circle Theorems Calculator

The circle theorems calculator is the perfect tool to understand the multiple geometric relationships between the parameters of a circumference and external parameters, such as tangent or secant lines 📐.

We've grouped all of the most important circle theorems in this simple calculator for you to better understand and practice this subject. We also paired this calculator with a short text describing, but not limited to, the following:

• What the circle theorems are;
• What the inscribed angle theorem formula is;
• The exterior angle of a circle theorem, also called the intersecting secants theorem;
• How to find the angles in a cyclic quadrilateral;
• The tangent to a circle formula; and
• More!

The circle theorems are a way to explain many mathematical properties and relationships between circles and all kinds of angles and line segments you can form with them. These theorems are usually taught to high school students as a way to simplify more complex geometry theorems.

In this circle theorems calculator, we've gathered six of them to aid in your studies regarding the circle theorems. Depending on who you ask, there might be a couple more theorems, but these are the ones that are easier to explain with a calculator.

In this tool, you will find:

• The inscribed angle theorem;
• The Thales theorem;
• The cyclic quadrilateral theorem;
• The equidistant chords theorem;
• The intersecting secants theorem; and
• The tangent to a circle theorem.

The inscribed angle theorem states:

• The inscribed angle is half the central angle which subtends the same arc; and
• Angles on the circumference subtended by the same arc are equal.

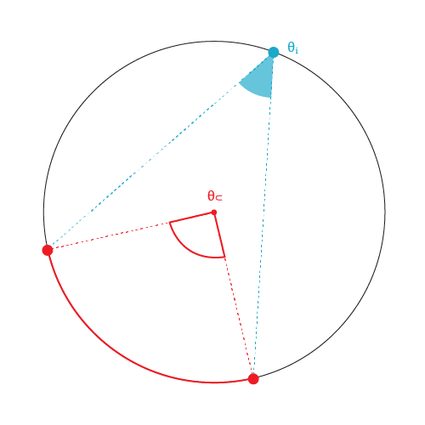
For example, if $\theta_i$ was an angle subtended by an arc (both within the circumference of the circle), and we measured the angle subtended by the same arc from the center of the circle ($\theta_c$), it will be twice the first angle.

Also, if another angle on the circumference were to subtend the same arc as $\theta_i$, according to the theorem, they would be equal.

Below is the inscribed angle theorem formula:

You can either manually use the inscribed angle theorem formula or input the angle in our circle theorems calculator using any unit. Give it a try!

Thales theorem states:

• If $A$, $B$, and $C$ are three points on the circumference of a circle, and $\overline{AC}$ lies on its diameter, then the angle $\angle ABC$ is a right angle.

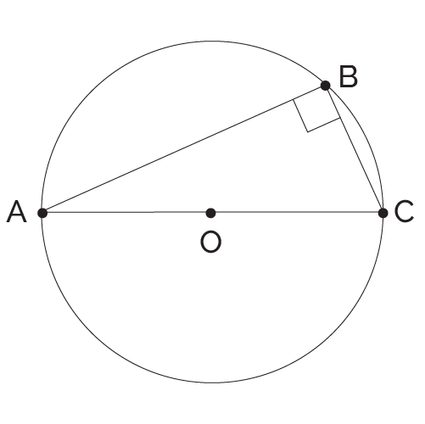
This is especially useful if we pair it with the Pythagorean Theorem because it allows us to find the missing angle or side. Since we already know the value of one angle ($90°$) and the hypotenuse (the diameter), we can easily find the rest if we know the value of one additional side or angle by doing a bit of arithmetics.

The next theorem is the cyclic quadrilateral theorem.

What is a cyclic quadrilateral? A cyclic quadrilateral is simply any quadrilateral whose vertices lie on the circumference of a circle.

This theorem says:

• Any two opposite angles in a cyclic quadrilateral add up to 180°.

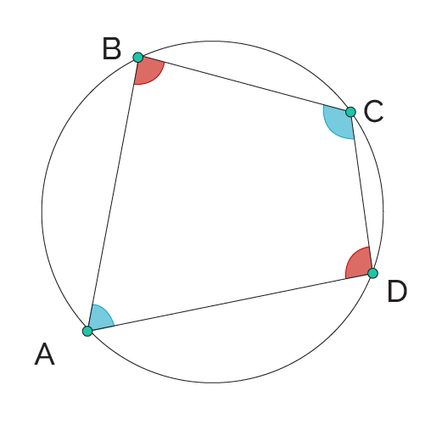
If we take the blue angles in this image, they will add up to 180°. The same applies to the red angles.

This theorem is straightforward:

• Chords equidistant from the center of a circle are equal in length.

This means that if you take any two chords of a circle that are equally separated from its center, they will also be equal in length. The reverse also applies: if two chords are equal, they will be equidistant to the circle's center.

We summarize this in the following expression:

where:

• $\overline{AB}$ is the length of a segment connecting any two points on a circle's circumference;
• $d$ is the distance of this segment to the circle's center; and
• $r$ is the radius of the circle.

You can find any parameter by rearranging this equation!

You can comprehend where this equation comes from by taking a look at the image below:

In this image:

• $\overline{OP}$ is the distance from the circle's center to the chord, $d$.
• $\overline{AB}$ is the chord's length.
• $\overline{OB}$ is the circle's radius, $r$.
• You can see that together these segments form a right triangle with $\frac{\overline{AB}}{2}$ and $d$ as its sides and $r$ as its hypotenuse. From here, you only need to utilize the Pythagorean theorem to get to the previous equation!

Also called exterior angle of a circle theorem, this theorem holds the relationship between a circle's interior and exterior angles formed by two secant lines. At the same time, it states the proportion between the intersection of these lines and its distance to the intersection of each line and the circle's circumference:

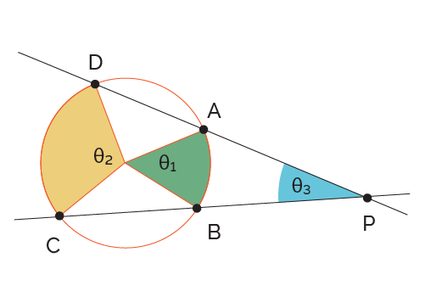
• If two secant lines intercept outside a circle, the angle subtended by the intersection is equal to half the difference between the furthest arc and the closest arc; and

• $\overline{PA} · \overline{PD} = \overline{PB} · \overline{PC}$.

The first statement translates to the following formula:

With our circle theorems calculator, you can find either the missing angle or the missing segment by simply typing in the values for the others.

The last theorem we will cover in our circle theorems calculator is the tangent to a circle theorem:

• A line tangent to a circle is perpendicular to the radius at the point of tangency.

This means that every line tangent to a circle will necessarily be perpendicular to a line from the center of the circle to the point of tangency.

With our calculator, you can input any point that lies on a circle's circumference, and it will instantly output the equation for a line tangent to the circle at that point.

Or, you can manually find the expression for the tangent line by replacing the values for $x$ and $y$ in the following equation:

and then, use $m$ to obtain:

where $m$ and $b$ are the gradient and y-intercept of the tangent line equation $y = mx + b$.

A cyclic quadrilateral is any four-sided polygon with all its vertices lying on a circle's circumference. Opposite angles within a cyclic quadrilateral add up to 180°. This is the main property of the cyclic quadrilateral theorem.

To find the length of a chord in a circle, follow these steps:

1. Write down the chord length formula: c = 2 · √(r² - d²). Here:
   • r is the radius;
   • c is the chord's length; and
   • d is the chord's distance to the circle's center.
2. Replace r and d with their respective values.
3. The result will be the length of any chord at that distance from the circle's center.

They are equal. According to the inscribed angle theorem, any inscribed angle will be equal to any other angle subtended by the same arc.

Yes, the tangent is always perpendicular to the circle's radius at the point of tangency. This is described by the Tangent to a circle theorem, which is one of the main circle theorems.

124°. Since opposite angles within a cyclic quadrilateral are supplementary, subtracting any of two opposite angles from 180° will return the other.