Bilinear Interpolation Calculator

Welcome to Omni's bilinear interpolation calculator! Are you a bilinear interpolation professional? Or rather wondering what bilinear interpolation is all about? Here you can find a brief overview of the bilinear interpolation method as well as a detailed explanation and derivation of the formula for bilinear interpolation.

As a bonus, we provided an example of how to perform bilinear interpolation by hand.

Bilinear interpolation is a popular method for two-dimensional interpolation on a rectangle. That is, we assume that we know the values of some unknown function at four points that form a rectangle. Let these points equal (x₁, y₁), (x₁, y₂), (x₂, y₁) and (x₂, y₂) and the values of the function are the following:

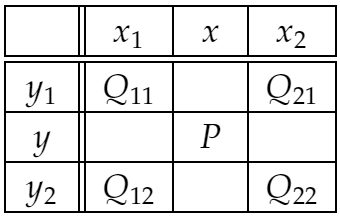
• The value at (x₁, y₁) is Q₁₁;
• The value at (x₁, y₂) is Q₁₂;
• The value at (x₂, y₁) is Q₂₁; and
• The value at (x₂, y₂) is Q₂₂.

Using bilinear interpolation, we can estimate this function's value at any point (x, y) inside this rectangle. We will denote this unknown value by P.

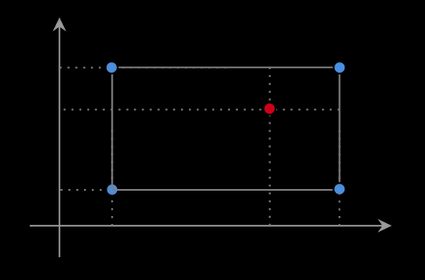
This interpolation scheme is widespread and has many applications, in particular in computer vision and image processing. It is based on a much simpler and widely taught procedure of linear interpolation, which you can discover with the help of Omni's linear interpolation calculator. For details, see the sections below.

It's worth knowing that the data required for bilinear interpolation is often collected in the form of the following table. Compare it to the plot above to see how smart the design of this table is!

Using this calculator is straightforward:

1. Enter the data:

   • x₁, y₁, x₂, y₂ for the coordinates of the base points of interpolation;

   • Q₁₁, Q₁₂, Q₂₁, Q₂₂ for the values at these points; and

   • x, y for the point at which we want to interpolate the unknown function by means of bilinear interpolation

2. That's it! Our bilinear interpolation calculator returns the result, i.e., the value of P at (x, y). A piece of cake, isn't it? 🍰

The general idea of the bilinear interpolation method is the following:

• Start by performing two linear interpolations in the x-direction (horizontal): first at (x, y₁), then at (x, y₂).
• Next, perform linear interpolation in the y-direction (vertical): use the interpolated values at (x, y₁) and (x, y₂) to obtain the interpolation at the final point (x, y).

Let's have a look at the details.

1. We find the linear interpolation of function f at (x, y₁) using the values of f at (x₁, y₁) and (x₂, y₁) which are Q₁₁ and Q₂₁ respectively:

2. We find the linear interpolation of f at (x, y₂) using the values of f at (x₁, y₂) and (x₂, y₂) which are Q₁₂ and Q₂₂ respectively:

3. Finally, we find the linear interpolation at (x, y) using the interpolated values of f at (x, y₁) and (x, y₂):

All that's left to do is to rewrite the above expression for P to get rid of the intermediate values R₁ and R₂.

• Substituting the expressions for R₁ and R₂ from Steps 1 & 2, we get the following formula for P:

• Using vectors and matrices, we can rewrite the above bilinear interpolation formula for P into the following form:

Tip: You may want to use to our matrix multiplication calculator while using the matrix form of the bilinear interpolation formula.

That was lots of theory, wasn't it? If you feel a bit overwhelmed, don't worry! In this section, we'll solve an example to show you how to use the bilinear interpolation formula in practice.

Assume that an unknown function has:

• Value 12 at (0, 1);
• Value -4 at (0, 3);
• Value 0 at (4, 1); and
• Value 8 at (4, 3).

We want to estimate the value of this function at (1, 2).

1. Let's begin by writing down some data.

   • For the rectangle corners, we have:

     x₁ = 0, x₂ = 4, y₁ = 1, and y₂ = 3

   • The respective function values are:

     Q₁₁ = 12, Q₂₁ = 0, Q₁₂ = -4, and Q₂₂ = 8

   • The point at which we perform the bilinear interpolation is:

     x = 1, y = 2

2. Let's calculate the terms that appear in the bilinear interpolation formula for P:

   • (x₂ - x₁) × (y₂ - y₁) = (4 - 0) × (3 - 1) = 8

   • (x₂ - x) × (y₂ - y) = (4 - 1) × (3 - 2) = 3

   • (x - x₁) × (y₂ - y) = (1 - 0) × (3 - 2) = 1

   • (x₂ - x) × (y - y₁) = (4 - 1) × (2 - 1) = 3

   • (x - x₁) × (y - y₁) = (1 - 0) × (2 - 1) = 1

3. Let's put those values together into the formula for P. We obtain:

   P = 3/8 × Q₁₁ + 1/8 × Q₂₁ + 3/8 × Q₁₂ + 1/8 × Q₂₂

4. It's time to substitute the values Q₁₁, Q₂₁, Q₁₂, and Q₂₂:

   P = 3/8 × 12 + 1/8 × 0 + 3/8 × (-4) + 1/8 × 8

5. Finally, we have:

   P = 9/2 - 3/2 + 1 = 4

Let's look once again at the final formula for P and point out some of its properties:

From this formula we see that:

1. Bilinear interpolation is

   • Linear with respect to the values Q₁₁, Q₁₂, Q₂₁, and Q₂₂ of the unknown function at the corners of the rectangle;

   • Linear along every horizontal line (where x changes and y is constant) and along every vertical line (where x is constant and y changes); but

   • Quadratic with respect to the location of the interpolation point, i.e., as a function of both x and y.

2. Bilinear interpolation is the weighted average of the values Q₁₁, Q₁₂, Q₂₁, and Q₂₂ at the four corners of the rectangle, and the weights are determined by the distance between the corners and the point (x, y). The closer a corner is to (x, y), the more weight that corner gets. See the weighted average calculator to learn more.