Surface Area of a Hemisphere Calculator

Our surface area of a hemisphere calculator is a handy tool that finds different types of hemisphere surface areas. Are you looking for an answer to the question of how to find the surface area of a hemisphere? Or maybe you just need to estimate it quickly? Whatever you plan to do, try this hemisphere calculator that comprises various area of a hemisphere formulas.

Hemispheres are created by dividing a sphere into two equal halves, as you can see in the picture below. Unlike the full sphere, a hemisphere has two kinds of surface areas: the base area (which is a circle) and the cap area. The notation, which we have used in this surface area of a hemisphere calculator, is as follows:

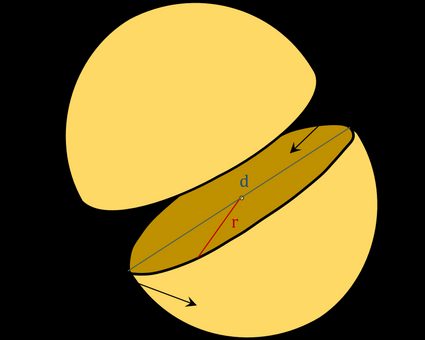
• r — Radius of a hemisphere;
• d — Diameter of a hemisphere;
• V — Volume of a hemisphere;
• A — Total surface area of a hemisphere;
• Ab — The base surface area of a hemisphere;
• Ac — Cap surface area of a hemisphere; and
• A / V — Surface-to-volume ratio of a hemisphere.

In case you need to analyze full spheres, our sphere calc is essentially the tool you're looking for!

When we split a sphere in half and take one of the resulting parts, we get a hemisphere. In each hemisphere, we can name two surface areas: base and cap areas (see the picture above). From the area of a sphere calculator, we know that the surface area of a sphere is as below:

A(sphere) = 4 × π × r²

You can think about it as two times the cap surface area of a hemisphere. Therefore, the hemisphere cap area equals:

Ac = A(sphere) / 2

Ac = 2 × π × r²

The base surface area is a circle with the same radius as a hemisphere. Thus, according to the circle calc: find A, it can be expressed as:

Ab = π × r².

Finally, the total surface area is the sum of those two contributions:

A = Ac + Ab

A = 2 × π × r² + π × r²

A = 3 × π × r²

This area of a hemisphere calculator allows you to find all three types of surface areas of a specific hemisphere. Moreover, you can do every calculation in different units (SI and imperial). If you want to learn more about area unit conversion, check out our area converter!

Now, after we know what the surface areas of a hemisphere are and how to find them, let's try to derive the different area of a hemisphere formulas. They can be useful in situations when we don't have the radius given. First of all, there are some basic hemisphere equations you should know:

1. Diameter of a hemisphere: d = 2 × r.
2. Volume of a hemisphere: V = 2/3 × π × r³.
3. Base surface area of a hemisphere: Ab = π × r².
4. Cap surface area of a hemisphere: Ac = 2 × π × r².
5. Total surface area of a hemisphere: A = 3 × π × r².
6. Surface to volume ratio of a hemisphere: A / V = 9 / (2 × r).

The area of a hemisphere formula (for the total area) can then be derived from the above equations. We can obtain even six of them! The equations used by this area of a hemisphere calculator are as follows:

1. Given radius: A = 3 × π × r²;
2. Given diameter: A = 3/4 × π × d²;
3. Given volume: A = ³√[243/4 × π × V²];
4. Given base area: A = 3 × Ab;
5. Given cap area: A = 3/2 × Ac; and
6. Given surface to volume ratio: A = 243 × π / (4 × (A/V)²).

As you know, the Earth is approximately a sphere with a radius of almost 6400 km, in which we can specify the northern and the southern hemispheres (specifically speaking, the Earth is a geoid). This division plays an essential role in geography and physics. For example, there is a force called the Coriolis effect, which acts on you whenever you travel by airplane, causing you to get off the course. When you're in the northern hemisphere, you will deflect to the right, and in the southern hemisphere, to the left. You can find more information about this topic in our Coriolis effect calculator.