Area of a Sphere Calculator

Q: What is the surface area of a sphere with a diameter of 8 cm?

The surface area of a sphere with a diameter of 8 cm is 201.06 cm 2 . To obtain this result, follow these steps: Multiply the diameter by itself to get the diameter squared : d 2 = 8 2 = 64 cm 2 . Multiply the diameter squared by pi to obtain the sphere's surface area: A = π × d 2 = π × 64 cm 2 ≈ 201.06 cm 2 . Verify the result using our area of a sphere calculator .

Q: How to find the surface area of half a sphere?

Since the surface area of a sphere of radius r is 4⋅π⋅r 2 , the surface area of half a sphere (also known as hemisphere ) would be: A = 4⋅π⋅r 2 /2 = 2⋅π⋅r 2 Including the circular base of the hemisphere, the surface area would be: A = 2⋅π⋅r 2 + π⋅r 2 = 3⋅π⋅r 2

Creators

Dominik Czernia, PhD

Dominik Czernia

PhD, Institute of Nuclear Physics PAN

Website

Research Gate

Dominik Czernia, PhD, is a physicist at the Institute of Nuclear Physics in Kraków, specializing in condensed matter physics with a focus on molecular magnetism. He has led several national research projects, pioneering innovative approaches to novel materials for high technology. Passionate about making science accessible, Dominik has created various calculators, mostly in physics and math categories. In his free time, he enjoys family walks, city explorations, mountain hiking, and traveling everywhere by bike. See full profile

Check our editorial policy

Reviewers

Bogna Szyk and Adena Benn

Adena Benn

Website

Adena Benn is a Guyanese teacher with a degree in computer science who is always reading and learning. She loves problem-solving, everything tech, and working with teenagers. She has a passion for education and is especially interested in how children learn and the teaching methods that best suit their learning styles. She grew up on a farm in Pomeroon, Guyana, where she worked alongside her parents and siblings. As such, she is just as comfortable growing plants as teaching in the classroom. In her early life, she also gained expertise as a seamstress, which she learned from her mother. By grade 9, she had already acquired her dressmaker's certificate. Today she uses her skills to design many items for her family. In her free time, Adena loves to read, take long walks, write children’s stories and poetry, travel, or spend time with her family. See full profile

Check our editorial policy

New

With our area of a sphere calculator, you can analyze every parameter of a sphere you want, but it is chiefly dedicated to its surface area. How to find the area of a sphere? If you only want to estimate its value, enter one of the chosen quantities into the right field. However, if you want to learn about the area of the sphere formulas, keep reading.

A sphere is a three-dimensional (3D) object, the contours and plane sections of which are circles. In other words, all of the points on the sphere are at the same distance from a fixed point (center). This area of a sphere calculator uses many quantities, and the notation is as follows:

r - radius of a sphere;
d - diameter of a sphere;
V - volume of a sphere;
A - area of a sphere; and
A / V - surface-to-volume ratio of a sphere.

A sphere is a special object that has the lowest surface-to-volume ratio among all other closed surfaces with a given volume. It is just like a circle that encloses the largest area with a given perimeter compared to the other flat figures. If you want more general information about spheres, head to the sphere calc!

We can divide any sphere into two equal parts, which are called hemispheres. Equations that describe hemispheres are very similar to those we have presented below for a full sphere. Are you curious what are properties of the hemispheres? Check out our area of a hemisphere calculator to learn more about that kind of object!

How to find the area of a sphere?

The first person who answered the question of how to find the area of a sphere was the ancient Greek - Archimedes. He discovered that the orthogonal projection from the lateral area of a cylinder onto the sphere keeps its area. Looking at the picture below, you can see that both objects have the same radius r, and the height of a cylinder equals the diameter of a sphere d. Therefore, using the lateral surface area of a cylinder formula, we obtain the following:

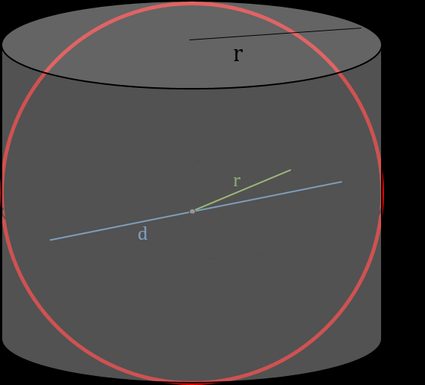
A = 2 × π × r × h;

A = 2 × π × r × d, and since d = 2 × r:

A = 2 × π × r × 2 × r; and

A = 4 × π × r²,

which is a well-known area of a sphere formula. If you want to see similar considerations for the radius, visit the radius of a sphere calculator.

What is the area of a sphere formula?

The above-presented area of a sphere formula is written in terms of radius. However, how to find the area of a sphere when we don't have the radius r but a different quantity that describes that sphere? First, let us remind you of the equations for those possible quantities:

Diameter of a sphere: d = 2 × r;
Volume of a sphere: V = 4/3 × π × r³; and
Surface to volume ratio of a sphere: A / V = 3 / r.

Now we can try to derive various surface areas of sphere formulas. In this area of a sphere calculator, we use four equations:

Given radius: A = 4 × π × r²;
Given diameter: A = π × d²;
Given volume: A = ³√(36 × π × V²); and
Given surface to volume ratio: A = 36 × π / (A/V)².

Our area of a sphere calculator allows you to calculate the area in many different units, including SI and imperial units. Also, if you want to learn how to estimate the surface areas of other figures, check out our surface area calculator, which is a more general tool.

FAQs

How do I find the surface area of a sphere, given its volume?

To find the surface area (A) of a sphere from its volume (V), follow these steps:

Multiply the volume by itself to obtain the volume squared: V².
Multiply this by 36 and pi to get:

36 × π × V².
Take the cube root of this expression to obtain the surface area of the sphere:

A = ³√(36 × π × V²).

Do these steps seem tedious? Our area of a sphere calculator can help you skip them and get the answer much faster!

What is the surface area of a sphere with a diameter of 8 cm?

The surface area of a sphere with a diameter of 8 cm is 201.06 cm². To obtain this result, follow these steps:

Multiply the diameter by itself to get the diameter squared:

d² = 8² = 64 cm².
Multiply the diameter squared by pi to obtain the sphere's surface area:

A = π × d² = π × 64 cm² ≈ 201.06 cm².
Verify the result using our area of a sphere calculator.

How to find the surface area of half a sphere?

Since the surface area of a sphere of radius r is 4⋅π⋅r², the surface area of half a sphere (also known as hemisphere) would be:

A = 4⋅π⋅r²/2 = 2⋅π⋅r²

Including the circular base of the hemisphere, the surface area would be:

A = 2⋅π⋅r² + π⋅r² = 3⋅π⋅r²

What is the radius of the sphere whose volume and area are equal?

The radius of the sphere whose volume and surface area are equal is 3 units. To find this answer, follow these steps:

Let the radius of this sphere we seek be r.
Equate the sphere's volume to its surface area to get the equation:

4⋅π⋅r³/3 = 4⋅π⋅r².
Divide both sides by 4⋅π⋅r² to get:

r/3 = 1.
Multiply both sides by 3 to get the radius value:

r = 3.