Scale Calculator

This scale calculator, also known as scale conversion or scale factor calculator, helps you to find the scale between two objects or the size of scaled/real structures for a given scale. Read on to find the answer to the question "What is a scale factor?", learn how to find a scale factor, discover that the scale conversion has a lot in common with length conversion, and forget about struggling with scales!

The scale factor can be defined as a ratio between two numbers (that you can find out more about in the ratio calculator). It can be both greater or lower than unity, depending on whether the scaled object is magnified or contracted.

The concept of a scale is extensively used in numerous fields, for instance, mathematics, geography, or economy. We can usually find scales while reading the instructions of a scaled model or a city map.

There are various ways in which we can present the scale:

• Numerical scale — It's dimensionless, and the form 1:1000 denotes that the scale factor equals 0.001. Any ratio of two numbers is correct, but it's common to take one of them as 1, e.g., 2.5:1 instead of 5:2. If, in the simplified form, one of the numbers isn't an integer and, simultaneously, is smaller than 10,000, it's worth considering the accuracy of a notation.

  In this scale calculator, we recommend using up to 5 significant figures if some of them are decimals or leaving the result rounded to the nearest integer. We may use a numerical scale to calculate vertical exaggeration, emphasizing particular objects on 3D maps and drawings. Check our vertical exaggeration calculator for more details!

• Lexical scale — Expressed in words, e.g., "one centimeter to one kilometer" or equivalently 1 cm : 1 km. We use them mostly with maps, and the conversion tells that 1 cm on the graph corresponds to 1 km of an actual distance. We can also meet a description that points out the size of the scaled object as a percentage of a real one.

• Linear (graphic) scale — Shows the object's dimensions or map in a graphical way. This representation is really natural and intuitive. Putting the scale from point A to point B tells you immediately the distance between them. You don't need to make any calculations! Even if you want to reprint a map with such a scale into a larger format, it won't be a problem because the scale will also be automatically magnified.

  In the example below, if we assume that the distance between major ticks equals 1 cm, it corresponds to 1 km of a real length, and then the scale is equivalent to 1 cm : 1 km or 1:100,000.

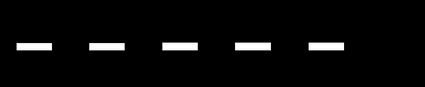
Graphic scales don't have to be a link between the same physical quantities. For example, the distance between adjacent ticks can denote a time interval of one second. You can find this type of conversion on a vast majority of charts.

In data analysis, it's sometimes worth considering the logarithmic scale. It's the ratio, instead of the difference, between neighboring ticks that is constant. That way, it's possible to juxtapose values in the range of several orders of magnitude in the same graph.

We often stick to some of the commonly used architectural scales in construction or landscaping projects. There is no need to learn them by heart, but it's really convenient to keep them in one place and know how to find the scale factor in every case. In the table below, we list several examples which can come in handy at some point:

You may be surprised, but the scale conversion for surfaces and volumes isn't as obvious as for distances. The scale usually tells about the ratio between the scaled and the original lengths, which means that every dimension has to change.

If we find that the scale factor equals f, then the ratio between the scaled and actual area will be f², and for the corresponding example with volumes, it will be f³.

Let's say you want to squeeze the circumference of a circle by a factor of 2. Then you can immediately conclude that the new area will be 4 times smaller. On the other hand, you may be wondering how to find the scale factor between two surfaces or volumes – just work out the ratio of scaled and real value, and the scale factor describing your model will be a square root for areas and a cube root for volumes.

In this scale factor calculator, you don't really have to worry about that fact. You can simply choose the option for which you want to find the scale.

Let's imagine that you've found a plan for your dream garden shed. On a scale model instruction, it is written that the length is 10 cm, the width is 8 cm, and the height is 5 cm. You want to build a structure with a length of 5 m, where the proportions of other dimensions are conserved.

1. Estimate the scale factor, 10 cm / 5 m = 0.02.

2. Write it down in the form of a numerical scale, 1:50, so that you remember the scale of your project.

3. Find the remaining dimensions – width: 8 cm / 0.02 = 4 m, height: 5 cm / 0.02 = 2.5 m.

4. You can evaluate the total volume of the shed so you can make sure that all your gardening equipment can fit inside: 5 m × 4 m × 2.5 m = 50 m³. You can also convert the volume into imperial units, which is about 65.4 yd³.

As you can see, it's a piece of cake to work out the final size of the shed's walls with a little help from our scale calculator. However, the overall appearance won't be imposing if the construction has only bare walls without a rooftop. You can change that, though – check out our roofing calculator and create a wonderful place in your garden!

To determine the distance between two objects based on their map distance:

1. Determine the distance between these objects on the map.

2. Apply the scale conversion formula: Map distance / Scale factor.

3. The result you get is precisely the real-world distance between the two objects.

A scale of 1:100 means that the map distance is 100 times smaller than the real-world distance. That is, 1 centimeter (0.01 meter) on the map corresponds to 100 cm (1 meter) out there in the real world.

100 meters. The scale 1:1000 means that 1 cm on the map corresponds to 1000 cm, which is 10 m. Therefore, 10 cm on a map means 100 m on the ground.