Astronomical Unit Calculator

Calculating the astronomical unit is a simple conversion exercise. However, with this knowledge, your understanding of the scale of the Solar System and our immediate stellar neighborhood will be much clearer. In this short article, you will learn:

• What is an astronomical unit: the meaning of this unit.
• How did scientists calculate the astronomical unit.
• The conversion between the astronomical unit and meter, kilometer, mile, etc.
• Astronomical unit vs. light years.
• And much more!

An astronomical unit, symbol $\mathrm{au}$, is a measurement unit for length used especially in astronomy as it originates in the distance between Earth and the Sun. The definition of astronomical unit, accepted by the International Astronomical Union (IAU) in 2012, fixes the exact conversion from astronomical unit to meters:

The astronomical unit is an average estimate of the distance between our planet and our star. It can't be otherwise: Earth's orbit, as every good planetary orbit, is not a circle, but an ellipse, even though the eccentricity (the deviation from the ideal circular orbit, as you can learn at our conic equation calculator) is extremely low. While the first definitions tried to use the average between the aphelion (the maximum distance between the Sun and Earth) and the perihelion (the minimum distance), astronomers eventually settled for an arbitrary yet significative value. But how did we measure this quantity?

How did we arrive at the value of 1 astronomical unit used by the IAU in the definition we've seen in the last section? The story is long!

Since antiquity, scientists have tried to assess the distance between the Sun and Earth, even when the understanding of celestial mechanics was close to zero. The first attempt, despite being bold and innovative, yielded poor results. We had to wait until the 17th century to finally see the first rigorous derivation of the distance between the Sun and Earth: Cassini and Richer, the same year of Flamstaad (1672) derived a value that is $0.925$ times the one accepted today.

What made this result possible? Parallax, together with constantly improving instruments. The parallax is an optical phenomenon in which by changing position relative to two objects, one distant and one much more distant, the first one moves, apparently by an angular distance that depends on a few geometric factors.

Hold an arm outstretched, extend a finger, and alternatively close and open each eye. You'll see your finger move across the background. The farther the background, the bigger the distance "covered" by your finger — though the angular distance remains the same. This is a practical example of parallax.

Scientists tried and managed to measure the solar parallax, the amplitude of the angle corresponding to Earth's radius at the Sun-Earth distance: you can understand this concept with the image below.

Once this angle is known, how do you calculate the astronomical unit? A tiny bit of trigonometry will go to great lengths, almost 150 million kilometers! As Earth's radius is known, and we now have the angle, we calculate the astronomical unit as:

where $r_\mathrm{Earth}$ is Earth's radius, and $\theta_\mathrm{solar}$ the solar parallax.

As humans developed new methods to look at the sky and even started venturing into the vastness between planets, our ways of measuring an astronomical unit changed. Radar and telemetry helped refine this measurement.

The simple geometrical considerations that led to humanity's first estimates of the value of 1 astronomical unit vacillated with the evolution of physics: minor corrections due to relativity added to the difficulty of the measurement. Eventually, the IAU decided that additional efforts to refine the definition of the astronomical unit were unnecessary.

We already know how to calculate from astronomical unit to meter, or at least; we know the conversion factor. To convert from astronomical units to meters, simply multiply the distance in au by the conversion factor. You can find even more conversions at our length converter.

Converting astronomical units to kilometers

To convert astronomical units to kilometers, divide the result of the previous conversion from au to m by $1000$. Converting from astronomical units to kilometers results, at least for the inner Solar System, in measurements still somewhat understandable: the minimum distance between Earth and Mars is a surprisingly low $0.37\ \mathrm{au}$. This value, in kilometers, is:

From astronomical units to miles

To convert from astronomical units to miles, you can remember the conversion factor:

which you can approximate to one hundred million miles with an error of less than 10%.

Astronomical unit vs. light year

Both the astronomical unit and the light year are measurement units fit for space. But space is unfathomably vast! With a rather elegant definition, the light year corresponds to the length covered by light in the vacuum in a year. The closest star to us, Proxima Centauri lies at $4.2465$ light years, while Polaris is $323$ light years apart. Our galaxy has a diameter of approximately $100,\!000$ light years. You can learn more at our dedicated light year calculator.

The astronomical unit, on the other hand, is fitting for interplanetary distances. If the light year is the distance covered by light in a year, the astronomical unit is the distance covered in 8 minutes 20 seconds.

To convert from astronomical units to light years, we use the following equation:

Or, in the opposite direction:

So, how far is Proxima Centauri in astronomical units?

The parsec is another length measurement unit used in astronomy. The parsec and the astronomical unit are tightly connected, constituting the legs of an imaginary right triangle built in space: the shorter leg is the astronomical unit, while the longer leg is the parsec. You can see this triangle in the image below.

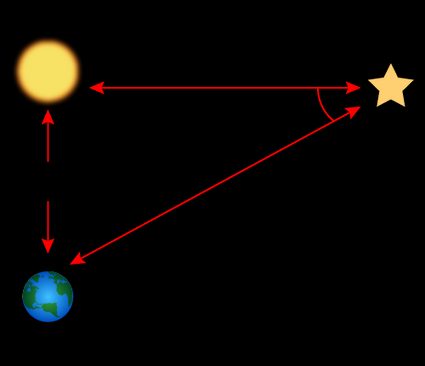
The acute angle farther from Earth has a fixed amplitude — in fact, this amplitude defines the value of the parsec. The angle is equal to exactly one arcsecond. As the construction is similar to the one used in parallax measurements, the name chosen for this unit reflected this fact: parallax of one second. Using basic trigonometry, we can find the value of the parsec:

Or, in other terms, to:

That equals, approximately:

The parsec is approximately equal to $3.26$ light years, making it ideal for intra- and intergalactic measurements.

Roughly one! The correct answer to the question "how many astronomical units is Earth from the Sun" depends on the moment of the year you ask it:

1. At the perihelion, the distance between Earth and the Sun is at the minimum and equal to 0.9832899 au.
2. At the aphelion, the distance is maximum and equal to 1.0167103 au.

Notice how the average of these measurements is roughly 1.

Jupiter's distance from the Sun in astronomical units is approximately 5.2 astronomical units away from the Sun. That's more than five times the distance between Earth and the Sun.

To find this distance in kilometers, multiply it by the conversion factor 1 au = 149,597,870.7 km:

d = 5.2 au × 149,597,870.7 km/au = 777,908,927.64 km.

To convert from astronomical units to km:

1. Remember the definition of astronomical unit: 1 au = 149,597,870,700 m.
2. Multiply the measurement in astronomical units by the factor of step 1.
3. Divide by 1000 to find the corresponding measurement in kilometers

No: the astronomical unit is not an SI unit but a particular measurement unit explicitly used in planetary astronomy. The value of the astronomical unit is fixed to 149,597,870,700 m, making it clumsy for everyday-life scale measurement and interstellar distances. However, all the distances between bodies in the Solar System are relatively small multiples of the astronomical unit, which made for a swift adoption of this unit.