Quadratic Regression Calculator

Our quadratic regression calculator is here whenever you need to determine the quadratic regression model of a data set. In other words, it allows you to answer the question: "What is the quadratic regression equation that fits these data?"

What is the quadratic regression model? In the sections that follow we provide you with the quadratic regression formula and explain how to calculate quadratic regression by hand!

If only want to find the roots of a quadratic equation, check out our quadratic formula calculator, which is a tool designed for solving this problem in particular.

There are situations where data doesn't quite follow a straight line, but instead a parabola seems to be just right:

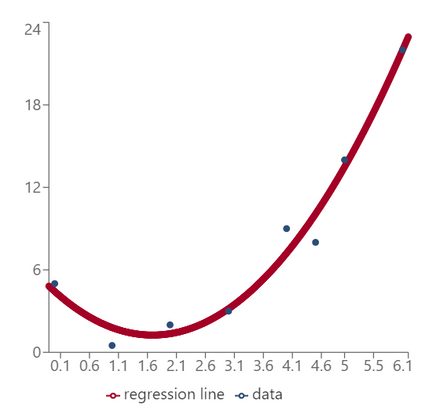
Quadratic regression helps you find the equation of the parabola that best fits a given set of data points. This is very similar to linear regression, where we look for a straight line, to cubic regression, where we deal with curves of degree three, or to exponential regression, where we fit exponential curves to data. If you need higher-degree polynomials, then try the polynomial regression calculator.

Let x be the explanatory variable and y the response variable.
The aim of quadratic regression is to find an equation in the form:

y = a + bx + cx²,

that best fits our data points

(x₁, y₁), ..., (x_n, y_n).

In the case of c = 0, the model boils down to a simple linear regression.

To compute the coefficients of the quadratic regression equation, we usually use the least-squares method. In this method, we determine the values of a, b, c so that the squared distance between each data point:

(x_i, y_i),

and the point:

(x_i,a + bx_i + cx_i²)

determined by the parabola equation:

y = a + bx + cx²

is minimal. We give the formulas in the next section.

If we have found a, b, c, we can measure how well the quadratic equation fits our data by calculating the coefficient of determination, R²:

where ȳ is the mean of y₁, ..., y_n.

R² assumes values between 0 and 1. The closer it is to 1, the better your quadratic regression model is at accurately representing your data. Discover more in our dedicated coefficient of determination calculator.

Well, there's gonna be lots of calculations to be made, but that's exactly what we love to do, don't we? 🙃

1. Deriving the quadratic regression formula is very simple: just calculate three averages:

2. Then we need to compute a whole bunch of sums:

3. We are almost there! The coefficients of the quadratic regression equation for our data are given by the following formulas:

4. As a bonus, here are alternative formulas for the expressions from Step 2. It's up to you to decide which ones look more friendly:

As you have seen in the previous section, it is a bit harder to calculate the quadratic regression by hand than finding the linear regression model yourself. That's why we have made this quadratic regression calculator, which performs all this tedious work for you in a blink of an eye!

However, if you still need to do this by hand and are unhappy with the formulas above, we have an alternative way. Namely, the coefficients a, b, c have to satisfy a system of three linear equations:

or, equivalently, in matrix form:

Hence, if you still are wondering how to calculate the quadratic regression, our answer is:

1. Compute the sum of x₁, ..., x_n and then the sums of their squares, cubes and fourth powers.
2. Then solve the system of three linear equations given above. Check our systems of equations calculator to read how to do this.

If you need to find out "what is the quadratic regression equation that fits these data", you can do it in no time with our quadratic regression calculator:

1. Enter your data: you can enter up to 30 data points (new rows will be appearing as you go). Remember that we need at least 3 points (both coordinates!) to fit a model. However, with exactly three points the fit is always perfect, as any three points determine the parabola!
2. A scatter plot with your data will appear underneath the data rows. We also add the parabola of best fit to the plot.
3. Below the graph, we display the quadratic regression equation for your data.
4. The coefficient of determination R² appears as well. It measures how well the derived model fits your data. It assumes values between 0 and 1, and the closer to 1 it is, the better the fit.
5. You can go to the advanced mode to increase the precision of calculations (number of significant figures). We set the default precision to four sig figs.