Possible Combinations Calculator

If you've ever wondered how to calculate combination possibilities, our possible combinations calculator is what you need.

This tool generates the number of all possible combinations, given a total number of objects and sample size. It also generates all the possible combination elements in a list.

As an example, to better understand the concept, we'll solve the common problem of knowing how many combinations of 5 letters are possible.

A combination is the number of ways you can choose r elements out of a set containing n distinct objects, no matter the order. If we must consider the order in which we obtain those elements, then we're dealing with permutations.

We know these definitions can sound complicated, and as a picture is worth a thousand words, we created the following graphic, which perfectly describes these concepts and their differences.

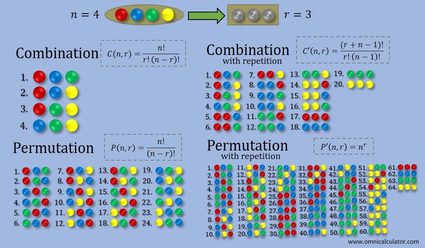
In the example of the image above, there are n = 4 balls of different colors, and the objective is to know how many distinct sets we can get by randomly sampling r = 3 elements.

As you can see, the combination process only considers sets with a different combination of elements each, no matter the order. In contrast, permutation additionally considers the various orders of a specific group of elements.

Also, there are two types of combinations and permutations: without repetition vs. with repetition. "With repetition" means we can have elements repeated within a group of r elements, while "without repetition" implies the opposite.

The following formula gives the number of possible combinations without repetition:

, where:

$C (n,r)$ — The number of possible combinations without repetition;
$n$ — The total number of objects;
$r$ — Sample size; and
$!$ — The factorial of the number to the left.

And if you're interested in how to calculate possible combinations with repetitions, this is the formula:

Now that you've learned the concepts let's see how to calculate how many combinations are possible through an example.

If you're interested in how to find all possible combinations, the easiest way is to use our calculator. Let's see an example.

Suppose you want to calculate how many combinations of 5 letters are possible. Follow these steps to discover it:

1. Identify the total number of objects (n) and the sample size (r).
   • Assuming we're dealing with the English alphabet (and not the Russian or the Chinese ones 😳), n = 26.
   • A combination of 5 letters means r = 5.
2. Go to the possible combinations calculator and input 26 in the "Total number of objects" box and 5 in the "Sample size" box.
3. That's it. The amount of possible combinations of 5 letters is 65,780 and 142,506 without and with repetition, respectively. Now you know how to calculate combination possibilities.

Now that you know how to generate all possible combinations with our calculator, you can take a look at these other tools:

• Combination calculator;
• Permutation and combination calculator;
• Combinations with repetition calculator; and
• Combinations without repetition calculator.

These are the possible combinations and permutations of forming a four-digit number from the 0 to 9 digits:

• Possible combinations:
  • Without repetitions: 210
  • With repetitions: 715
• Possible permutations:
  • Without repetitions: 5,040
  • With repetitions: 10,000

The possible combinations and permutations of arranging twelve numbers (i.e., the 1-12 number list) are:

• Possible combinations:
  • Without repetitions: 1
  • With repetitions: 1,352,078
• Possible permutations:
  • Without repetitions: 479,001,600
  • With repetitions: 8,916,100,448,256

The number of possible combinations without repetitions C(n,r) equals one because the total number of objects n (twelve digits) equals our sample size r (the twelve digits we'll arrange). In other words, if n = r, then C(n,r) = 1.