Combination without Repetition Calculator
Our combinations without repetition calculator finds the number of combinations without repetitions that are possible given the total number of objects and the sample size.
In the next section, we present the formula for combinations without repetition, which is the one this calculator uses. We also show an example of how to calculate combinations without repetition.
🙋 Important:
- Our calculator doesn't only calculate the number of combinations without repetition, but it also generates those combinations without repetition in a list.
- This calculator deals only with combinations. Please don't confuse it with permutations ⚠️
- We also have a permutation calculator 😉
Combination vs. permutation
Combinations and permutations are usually confused. Before using our calculator, it's essential to know the difference:
- Combination: The number of ways you can choose r elements from a set containing n distinct objects, no matter the order.
- Permutation: The number of ways you can choose r elements from a set containing n distinct objects, taking all the possible orders into account. Each possible ordering of the same group of elements accounts for an additional permutation.
As a picture is worth a thousand words, we created the following graphic, which perfectly describes these concepts and their differences.
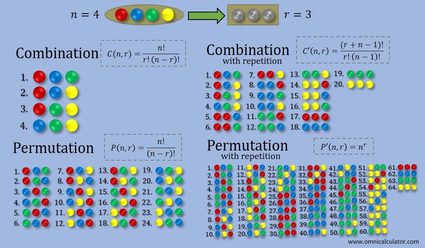
How do I calculate combinations without repetition?
The formula to calculate combinations without repetition is:
C(n,r) = n! / r!(n-r)!,
, where:
- C(n,r) — The number of combinations without repetition;
- n — The total number of objects (how many distinct objects you have); and
- r — Sample size (how many objects we want to choose).
Example: How many combinations of 4 numbers without repetition are possible?
Suppose you're interested in calculating the number of combinations without repetition from 4 numbers out of the decimal systems (numbers from 0 to 9) that are possible. Let's use the combinations without repetition formula to know the answer. Follow these steps:
- Identify the relevant values.
- We want combinations of 4 numbers; therefore, our samples are of size r = 4.
- The total number of objects comes from the decimal system (numbers from 0 to 9). Therefore, n = 10.
- In the formula of combinations without repetition, input the values:
- That's it! That's how you calculate the number of combinations without repetition. You can also check the answer with our combinations without repetition generator/calculator.
Other useful calculators
Now you know how to calculate and generate combinations without repetition. The next step is to look at these other tools we created:
- Combination calculator;
- Permutation and combination;
- Possible combinations; and
- Combinations with repetition.
In the following FAQ section, we solve some interesting problems, like how many combinations without repetition with 16 numbers or five digits are possible.
FAQs
How many combinations with 16 numbers without repetition are possible?
There's one (1) possible combination without repetitions and 300,540,195 combinations with repetitions of arranging a group of sixteen numbers (i.e., the 1-16 number list).
The possible combinations without repetitions C(n,r) is one because the total number of objects n (sixteen digits) equals our sample size r (the sixteen digits we'll arrange). In other words, C(n,r) = 1 because n = r.
How many combinations with 5 numbers without repetition are possible?
There's one (1) possible combination without repetitions C(n,r) and 126 combinations with repetitions C'(n,r) of arranging a group of five numbers (i.e., the 1-5 number list).
The number of possible combinations without repetitions equals one because the total number of objects n (five numbers) equals our sample size r (the five digits we'll arrange). In other words, if n = r, then C(n,r) = 1.