Last updated: Jul 17, 2024

Torsional Constant Calculator

Q: What is the difference between the polar moment of inertia and the torsional constant?

Both are a measure of the torsional stiffness of a beam, but there are some differences: With the polar moment of inertia, we can only calculate the angle of twist in circular members. With the torsional constant, we can calculate the angle of twist in beams with cross-sections beyond the circular geometry.

Q: What are the torsion constant units?

The torsional constant units usually used are mm 4 in the International System of Units and in 4 in the United States customary system. The m 4 and ft 4 units are also used, although less frequently.

Q: How do I calculate the torsional constant of a square section?

To calculate the torsional constant of a square section: Raise the square's side length to the fourth power . For example, for a 5 cm square: (5 cm)⁴ = 625 cm⁴ . Multiply the previous result by 9/64 . In the current example, the result would be (9/64) × 625 cm⁴ = 87.89 cm⁴ . That's it! You can also use our calculator and calculate the torsional constant of I-beams and many more shapes.

Q: How do I calculate the torsional constant of an I-beam?

For an I-section, the formula for the torsional constant ( K ) is: K = 2 K ₁ + K ₂ + 2 αD ⁴ , where: K ₁ = ab ³/3 - 0.21 b ⁴ - 0.0175 b ⁸/ a ⁴ ; K ₂ = cd ³/3 ; D = [( b + r )² + rd + d ²/4]/[2 r + b ] ; and α = ( t / t ₁)(0.15 + 0.1 r / b ) If b < d , then t / t ₁ = b / d ; and If d < b , then t / t ₁ = d / b . a is the flange width, b is the flange thickness, c is the web height, d is the web width, and r is the beam fillet radius. These formulas are valid as long as d < 2( b + r ) .

Created by Luis Hoyos

Luis Hoyos

Luis Hoyos is a fresh graduate Mechanical Engineer with thermodynamics and fluids mechanics expertise. He's interested in learning new things and applying them to real-life problems. Luis also likes to build tools that make repetitive and boring tasks a breeze, like calculators (surprise?). When he's not creating calculators, he's in the process of building the size of the tissue attached to his bones, aka bodybuilding. He also loves being with his little cat and seeing her do crazy things. See full profile

Check our editorial policy

Reviewed by Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

New

Table of contents

What is the torsional constant?Important things to consider when using this calculator Torsion constant formulas Example: How to calculate the torsional constant of a rectangle cross-section beam FAQs

If you were searching for how to calculate the torsional constant of I-beams and many other structural profiles, search no more!

When studying the behavior of beams subjected to torsion, we usually focus on circular bars. Still, sometimes it's necessary to go beyond, as some non-circular members can experience torsional loads (an example of this is the wing span of an aircraft). For this reason, we created this tool!

Keep reading to learn more about the torsional constant, what to consider when calculating the torsional constant, and the formulas behind this calculator.

🙋 Once you get the torsional constant, you can use it in our angle of twist calculator.

What is the torsional constant?

Besides shear modulus and beam length, the torsional constant (also known as the torsion constant) is one of the properties that describe the torsional stiffness of non-circular beams (similar to the polar moment of inertia). Opposite to shear modulus, it is a geometrical property, as it only depends on the form and dimensions of the cross-section.

As we saw in our polar moment of inertia calculator, to calculate the angle of twist of a beam under torsion using the polar moment of inertia, the cross-section of the member must remain plane and undistorted, which only occurs in circular sections.

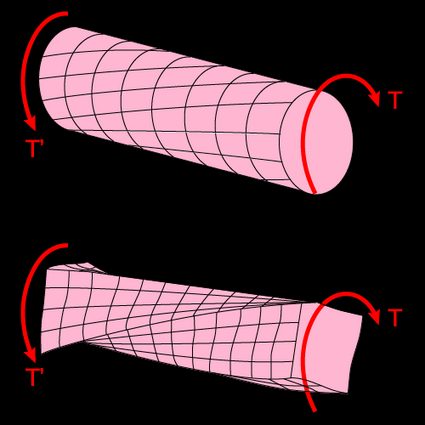
Comparison of the deformations obtained in circular and rectangular bars under torsion.

Fortunately, we can obtain analog expressions of the polar moment of inertia for different geometries using advanced solid mechanics procedures. The torsional constant is the property that allows us to calculate the angle of twist of non-circular bars:

\phi = \frac{TL}{KG}

In this equation:

$\phi$ — Angle of twist;
$T$ — Torque applied to the beam;
$L$ — Shaft length;
$G$ — Shear modulus of the shaft material; and
$K$ — Beam torsional constant, the one we get with this calculator.

The torsional constant in this formula has the same function as the polar moment in a circular beam, but we termed it here with the $K$ symbol to differentiate both.

Before looking at the formulas, let's see some aspects worth considering when using this tool and the equations.

Important things to consider when using this calculator

The formulas used in this calculator rely on the following assumptions:

The beam is straight and uniform.
The bar is loaded only by equal and opposite twisting couples, applied at its ends in planes normal to its axis.
The stress in the bar doesn't surpass the elastic limit.

🙋 The second condition implies that the end sections are free to warp (no forces to hold them in their respective planes). If that second condition doesn't hold (there are fixed ends or couples applied at sections other than the ends), the actual angle of twist will be different. How different? The effect is not that big in compact cross-sections, but the difference may be significant for open thin-walled members.

If you're interested in cases in which the second condition doesn't apply, you can look at section 10.3 of the work of Budynas & Sadegh.

Torsion constant formulas

The following are the torsion constant formulas behind this calculator. As you can note, the polar moment of inertia and the torsional constant are equal for circular profiles. Here are some notes about the accuracy of these formulas:

Although the thin-walled ellipse and thin-walled rectangle formulas rely on mathematical analysis, they possess an error that depends on how close the geometry conforms to the consequence of the second assumption of the previous section (not being an open thin-walled member).
The solid rectangle formula is a simplified version with an error no greater than 4%.
The formula for the I-beam relies on experimental methods, with (rarely) as much as a 10% error.

Form		K formula in $\phi = \frac{TL}{KG}$

Circle		$K = \frac{\pi r^4}{2}$



Solid ellipse		$K = \frac{\pi a^3b^3}{a^2+b^2}$



Hollow ellipse		$K = \frac{\pi a^3b^3}{a^2+b^2}(1-q^4)$
		$q = \frac{a_0}{a} = \frac{b_0}{b}$


Thin-walled ellipse		$\frac{4\pi^2 t(a-\frac{t}{2})^2(b-\frac{t}{2})^2}{U}$
		$U = \pi (a+b-t)\left[1+0.258\frac{(a-b)^2}{(a+b-t)^2}\right]$



Solid square		$K = \frac{9}{64} a^4$



Solid rectangle		For a≥b
		$K = \frac{a b^3}{3} - 0.21 b^4 + 0.0175 \frac{b^8}{a^4}$
		$K = \frac{a b^3}{3} - 0.21 b^4 + 0.0175 \frac{b^8}{a^4}$

Thin-walled rectangle		$K = \frac{2t t_1(a-t)^2(b-t_1)^2}{at+b t_1-t^2-t_1^2}$



I-section		$K = 2 K_1+K_2+2\alpha D^4$
		$K_1 = \frac{a b^3}{3} - 0.21b^4 + 0.0175\frac{b^8}{a^4}$
		$K_2 = c d^3/3$
		$D = \frac{t}{t_1}(0.15+0.1\frac{r}{b})$
		$\alpha = \frac{t}{t_1}(0.15+0.1\frac{r}{b})$
		If b < d, then $\frac{t}{t₁} = \frac{b}{d}$
		If d < b, then $\frac{t}{t₁} = \frac{d}{b}$

Example: How to calculate the torsional constant of a rectangle cross-section beam

Suppose you want to calculate the torsional constant of a rectangular section with a base of 10 mm and a height of 5 mm. Follow these steps to get the answer:

Determine your "a" and "b" values to use in the formula. In this case, $a = 10 \rm\ {mm}$ and $b = 5\ \rm{mm}$ .
Input the "a" and "b" values in the corresponding formula:

\scriptsize \qquad \begin{align*} K &= \frac{a b^3}{3} - 0.21 b^4 - 0.0175 \frac{b^8}{a^4}\\[1em] &= \frac{10\ \rm{mm} (5\ \rm{mm})^3}{3} - 0.21 (5\ \rm{mm})^4 -\\[1em] &\quad\ \ 0.0175 \frac{(5\ \rm{mm})^8}{(10\ \rm{mm})^4}\\[1em] &= 284.73 \ \rm{mm}^4 \end{align*}

That's it! The torsional constant of that rectangular section is $284.73\ \rm{mm}^4$

FAQs

What is the difference between the polar moment of inertia and the torsional constant?

Both are a measure of the torsional stiffness of a beam, but there are some differences:

With the polar moment of inertia, we can only calculate the angle of twist in circular members.
With the torsional constant, we can calculate the angle of twist in beams with cross-sections beyond the circular geometry.

What are the torsion constant units?

The torsional constant units usually used are mm⁴ in the International System of Units and in⁴ in the United States customary system. The m⁴ and ft⁴ units are also used, although less frequently.

How do I calculate the torsional constant of a square section?

To calculate the torsional constant of a square section:

Raise the square's side length to the fourth power. For example, for a 5 cm square: (5 cm)⁴ = 625 cm⁴.
Multiply the previous result by 9/64. In the current example, the result would be (9/64) × 625 cm⁴ = 87.89 cm⁴.
That's it! You can also use our calculator and calculate the torsional constant of I-beams and many more shapes.

How do I calculate the torsional constant of an I-beam?

For an I-section, the formula for the torsional constant (K) is:

K = 2K₁ + K₂ + 2αD⁴,

where:

K₁ = ab³/3 - 0.21b⁴ - 0.0175b⁸/a⁴;
K₂ = cd³/3;
D = [(b + r)² + rd + d²/4]/[2r + b]; and
α = (t/t₁)(0.15 + 0.1r/b)
- If b < d, then t/t₁ = b/d; and
- If d < b, then t/t₁ = d/b.
a is the flange width, b is the flange thickness, c is the web height, d is the web width, and r is the beam fillet radius.

These formulas are valid as long as d < 2(b+r).