SUVAT Calculator

"But Sir," we hear you ask, "Why should I bother to learn all these SUVAT formulas when I can just go online, and use the SUVAT calculator?". Your teacher then obviously replies "Can that SUVAT equations calculator teach you what SUVAT stands for? Does it know all the SUVAT formulae, and can it use them to calculate the two unknowns in any situation? Does it provide you with a few SUVAT questions to check if you really know your stuff? Can you take it into your exam?" Well, you can tell your teacher that this calculator can do all of those things! (Omni Calculator does not recommend trying to bring this calculator into your exam, no matter how little revision you did.)

On the topic of exams, if you are a GCSE or A-level student and want to know how you did on a past paper, we recommend you check out our test grade calculator, while if you need to know how many marks you need on your final exam to get your desired grade, check out our final grade calculator.

To convert betweeen units, please use the built-in unit converters next to the input, or use our

• length converter,
• speed conversion, or
• time unit converter.

This is a simple kinematics calculator; for a complete tool, please visit projectile motion calculator.

There are five SUVAT formulas (or SUVAT formulae if you're feeling fancy). These five formulas describe everything there is to know about a system in motion, as long as it has uniform acceleration, that is. They are commonly used in physics, as they describe a wide range of systems. If you know the object's initial velocity u, it's final velocity v, and the time t it took to reach velocity v from velocity u, you can find the five SUVAT equations...

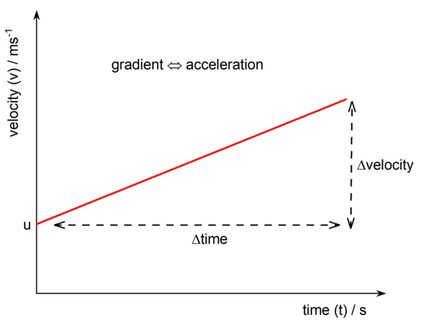
Above we plotted a graph of velocity vs. time, using the u, v, and t we discussed above. This means that acceleration, a, is the gradient of the straight line we drew. So:

As we know both the initial and final velocity, Δvelocity = v - u, and, if we assume that we began plotting the graph at time = 0, Δtime = t. Therefore you get

which can be rearranged to

If your interested in SUVAT, we're going to go ahead and assume you can do this rearrangement by yourself.

We are yet to mention displacement s in this SUVAT calculator. Displacement is the distance the object covers during time t with respect to its starting position. That last bit is important since displacement is not the same as distance; if it ends up at the spot that it started at, then its displacement is zero. On the velocity-time graph we plotted above, s is the area underneath the graph. As we have a linear plot, the area underneath it is found by multiplying the average velocity, (u + v) / 2, and the time taken, t. Writing this out and simplifying gives:

Sometimes it's useful to have more equations to work with; you never know which variables you will have. You can get the next equation by substituting v = u + at. The result is:

which simplifies to $s = \frac{1}{2} (2ut + at^2)$, which in turn can also be written as:

That one wasn't too difficult, just a bit of algebra, you must feel like you're thirteen again. To obtain the other form, follow the same steps as the last one, but use u = v - at instead:

As a kind of SUVAT question, we'll leave this one for you to derive yourself - we know that it won't be a problem for you.

The last SUVAT formula requires slightly more complex rearrangement, so maybe you'll feel like you're fourteen while doing this. If we make t the subject of the first equation we derived, we get:

which if we substitute into the second equation we derived, we end up with:

Multiplying both sides by 2a we get:

which now requires that most difficult of skills to master - quadratic expansion! So, after much blood, sweat and tears, you should end up with:

Rearranging for $v^2$ then gives you:

Wow, you really are a maths master!

So that's all of the SUVAT formulas. If you found this text dreadfully boring and incomprehensible (not too far out of the question), we recommend to you this Youtube video on the topic.

You have probably already guessed this from reading through this SUVAT calculator so far (if you can't guess, you may have just skipped all that mumbo-jumbo above). SUVAT is an acronym of the five variables that describe a system in motion with constant acceleration: displacement s, initial velocity u, final velocity v, acceleration a, and time t.

The order of these letters is totally arbitrary, so you can keep yourself up at night wondering why it's not called TUAVS, SAVUT, or USAVT (although we think it's probably best that initial and final velocity stay next to each other, so maybe ATUVS or STAUV are better).

"Okay, okay, okay," your teacher now says, "So you might have found a calculator that gives you the SUVAT equation, and yes, it might explain what SUVAT stands for, but that doesn't mean it can help you solve any questions!" Well, we can understand that he might be getting annoyed right about now - you've been holding up class for ten minutes while you load this page and show the class all of its amazing features. But what's probably annoying him the most is that you finished learning about SUVAT ages ago, and have now moved onto friction and the normal force (and that this is also a statistics class). But don't fret, we have prepared a few sample questions to help you get the most out of this SUVAT calculator.

1. You see your teacher getting angry at you. You decide it's time to run away. From rest, it takes you 4 seconds to reach the door, which is 7 m away. How fast are you going when you reach the door?
2. You stop as you open the door and go through it. You are now in the corridor. 50 m away is the door leading outside. You will be safe once there. You start running with a constant acceleration of $0.75~\mathrm{m/s^2}$. What is your velocity when you reach the door?
3. Two seconds after you set off down the corridor, the teacher bursts through the door, fuming. He again sets off from rest, and, powered by nothing more than pure hate at you showing him up in front of the whole class, begins accelerating at $2~\mathrm{m/s^2}$. Will he reach you before you can claim your freedom?
4. What about if the classroom door was open when you reached it, allowing you to conserve your velocity? If you began accelerating at $0.75~\mathrm{m/s^2}$ from this speed down the corridor, and the teacher still stops at the door (to see where you've gone), would you be free?

Answers: