Last updated: Aug 09, 2024

Dipole Moment Calculator

Q: How do I calculate the dipole moment of two oppositely charged particles?

If you have two charges q and -q at a distance d , you can measure an electric dipole momentum p equal to: p = q d Notice that both p and d are vectors . d points from the negative charge to the positive one, and p does the same as a consequence.

Q: Why is the electric dipole moment important in chemistry?

The electric dipole is a fundamental quantity in chemistry as it quantifies the behavior of bonds inside molecules . Since every atom attracts electrons in a bond with force given by the electronegativity specific to that element, the electrons are pulled more or less in a particular direction, causing the charge in the bond to be distributed unequally among the atoms. As the dipole is relatively easy to measure, we can use it to calculate quantities like the interatomic distance (much harder to measure).

Q: What is the dipole moment of two opposite charges of 0.5 C at 20 cm?

The dipole moment of two charges q and -q , with q = 0.5 C , separated by 20 cm , is p = q × d . To find this result: Convert the distance to meters : 20 cm ≡ 0.2 m . Multiply the charge by the distance: q × d = 0.5 C × 0.2 m = 1 C · m This is the dipole moment. Notice that, by definition, it points from the negative charge to the positive one (as it is a vector).

Created by Davide Borchia

Davide Borchia

Physicist by education, scientist by vocation. He holds a master’s degree in complex systems physics with a specialization in quantum technologies. If he is not reading something, he is outdoors trying to enjoy every bit of nature around him. He uses his memory as an advantage, and everything you will read from him contains at least one “I read about this five years ago” moment! See full profile

Check our editorial policy

Reviewed by Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

New

Table of contents

What is the electric dipole moment?Calculate the electric dipole moment for two identical charges How to calculate the dipole moment of a system of electrically charged particles Example of calculations of the electric dipole moment for a system of charges How to use our electric dipole moment calculator FAQs

Calculating the dipole moment of a system of charges gives you information on the polarity of a system. This quantity is fundamental in electrostatic: keep reading to learn more! In this article, you will learn:

What is the dipole moment of a system of charges?
How to calculate the dipole moment of two identical charges?
The formula to calculate the dipole moment of a system of charges.
How to calculate the electric dipole moment: an example.

And much more. You will surely find this tool useful!

🙋 For the almost homonymous quantity related to the magnetic field, visit our magnetic dipole moment calculator.

What is the electric dipole moment?

The electric dipole moment is a measure of the polarity of a system using an analysis of the present charges and the distance between them. The electric dipole moment is a vectorial quantity, which means it is associated with two quantities:

A direction; and
A magnitude.

In the case of the electric dipole moment, the direction is always from an accumulation of negative charge to the positive charge. At the same time, the magnitude measures how the distribution of charges affects a test charge between them, accelerating or decelerating it in the direction specified above.

The electric dipole is a fundamental quantity of chemistry, where many properties of a molecule depend on the distribution of electric charges inside it, which in turn depends on how strongly an atom attracts the electrons in a bond (we measure this attitude with the electronegativity: learn more about it at our electronegativity calculator and percent ionic character calculator).

The dipole moment is also relatively easy to measure, thus allowing for determining the distance between atoms via experimental methods: a quantity so small that baffles most attempts at measuring it directly!

With this short introduction, we can move to the mathematics of the problem. Let's learn how to calculate the electric dipole moment, starting from the simplest of systems.

Calculate the electric dipole moment for two identical charges

The most straightforward situation where we can calculate the electric dipole moment is when our system is composed of two identic charges with opposite signs, separated by a given distance. In this case, the dipole is simply the product of charge and distance, and we write this as:

\boldsymbol{p} = q\boldsymbol{d}

where:

$p$ — Electric dopole moment;
$q$ — Electric charge of one of the particles (consider the positive one in this situation); and
$d$ — Displacement vector or distance between the two charges.

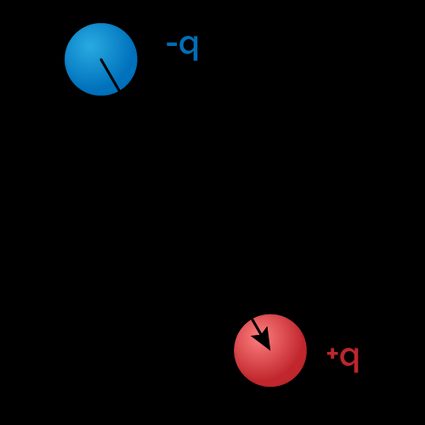
A system of two identical charges with opposite signs.

From this simple equation, we infer that the dipole moment is measured in coulomb-meters ( $\text{C}\cdot\text{m}$ ). We also notice that the equation is vectorial in nature: the dipole has the direction of the displacement vector, which originates in the negative charge and points toward the positive one.

How to calculate the dipole moment of a system of electrically charged particles

When dealing with an array of electrically charged particles, we can calculate the dipole moment of the system. In this case, the dipole moment will depend on the position we measure it. Let's introduce the quantities we will use in the formula to calculate the dipole moment of such a system:

$\boldsymbol r$ — Reference point in a Cartesian plane;
$q_i$ — Electric charge of the charge labeled $i$ ; and
$\boldsymbol r_i$ — Position of the charge labeled $i$ in the Cartesian plane.

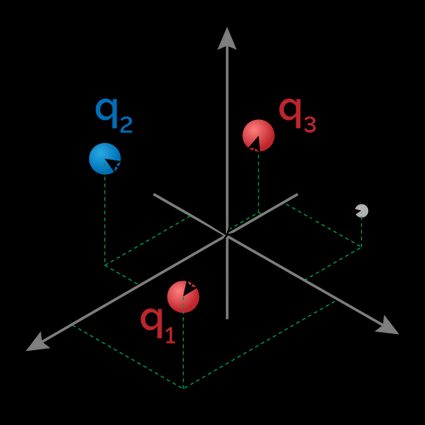
A system of charged spherical particles and a reference point.

The index $i$ varies from $1$ to $N$ , with $N$ being the number of charges in the system. For each of the charges, we compute the difference between the two position vectors:

\boldsymbol{d}_i = \boldsymbol{r}_i-\boldsymbol{r}

Notice how this quantity is nothing but the displacement vector from the point $\boldsymbol r$ to the charge $i$ . We used the rules to calculate the vector addition.

We subsequently sum over all the charges this way:

\boldsymbol{p}(\boldsymbol{r}) = \sum_{i=1}^N q_i \boldsymbol{d}_i = \sum_{i=1}^N q_i (\boldsymbol{r}_i-\boldsymbol{r})

The point $\boldsymbol{r}$ feels the presence of all the charges in the system.

Example of calculations of the electric dipole moment for a system of charges

Take a system with three charges:

$q_1 = 0.25\ \mathrm{C}$ at $\boldsymbol{r}_1 = (2,3,3)$ ;
$q_2 = -0.14\ \mathrm{C}$ at $\boldsymbol{r}_1 = (1,-1,1.5)$ ; and
$q_3 = 0.17\ \mathrm{C}$ at $\boldsymbol{r}_1 = (-1,-0.5,2)$ .

We assume the distances to be in centimeters. It won't matter till the end!

Take the reference point $\boldsymbol{r} = (-1.5,2.5,2)$ , and calculate the dipole moment in that position. We can expand the formula for the dipole moment of a system of charges since we are dealing with only three charges, and the result won't be too cumbersome:

\begin{split} \boldsymbol{p}(\boldsymbol{r}) &= \sum_{i=1}^N q_i (\boldsymbol{r}_i-\boldsymbol{r})\\[1.5em] &=q_1 (\boldsymbol{r}_1-\boldsymbol{r}) + q_2 (\boldsymbol{r}_2-\boldsymbol{r}) \\ &\quad+q_3 (\boldsymbol{r}_3-\boldsymbol{r}) \end{split}

Let's calculate the difference in vectors first:

\scriptsize \begin{split}(\boldsymbol{r}_1-\boldsymbol{r}) &= (2+1.5,3-2.5,3-2) \\&= (3.5,0.5,1)\\[1em] (\boldsymbol{r}_2-\boldsymbol{r}) &= (1+1.5,-1-2.5,1.5-2) \\&= (2.5,-3.5,-0.5)\\[1em] (\boldsymbol{r}_3-\boldsymbol{r}) &= (-1+1.5,-0.5-2.5,2-2) \\&= (0.5,-3,0)\end{split}

And substitute the result in the formula above:

\small\begin{split} \boldsymbol{p}(\boldsymbol{r}) &= 0.25\ \mathrm{C}\ (3.5,0.5,1)\\ &\quad -0.14\ \mathrm{C}\ (2.5,-3.5,-0.5) \\ &\quad+0.17\ \mathrm{C}\ (0.5,-3,0)\\ &=(0.875,0.125,0.25)\\ &\quad+(-0.35,0.49,0.07)\\ &\quad+(0.085,-0.51,0)\\ &=(0.61,0.105,0.32) \end{split}

This is the vector corresponding to the dipole moment in coulomb-centimeter.

How to use our electric dipole moment calculator

You can use our electric dipole moment to calculate the dipole moment in a simple symmetric two-charge system and a more complex system of unbalanced charges.

Choose the desired mode in the first selection of the tool. In the case of the simple two-charge system, fill in the desired fields to find the result. You can also use the calculator in reverse, inserting the dipole moment to find the distance or the charges.

If you desire to find the dipole moment of a system of charges, choose the corresponding mode in the top menu. Afterward, specify the coordinates of the reference point as well as the number of charges your system contains. Then, input the electric charge (q) and coordinates (x, y, z) for each charge, and we will calculate the dipole moment. You can insert up to five charges!

🙋 Don't confuse the electric dipole moment with the dipole antenna, even though it may happen that you will hear the former shortened to "dipole". Learn more about the latter at our dipole antenna calculator!

FAQs

What is the electric dipole moment?

The electric dipole moment measures the separation between positive and negative charges in a system of electric charges. The electric dipole moment measures the reaction of such a system when immersed in an electric field, where the field tries to align the dipole with the field by applying a proportional torque.

How do I calculate the dipole moment of two oppositely charged particles?

If you have two charges q and -q at a distance d, you can measure an electric dipole momentum p equal to:

p = q d

Notice that both p and d are vectors. d points from the negative charge to the positive one, and p does the same as a consequence.

Why is the electric dipole moment important in chemistry?

The electric dipole is a fundamental quantity in chemistry as it quantifies the behavior of bonds inside molecules. Since every atom attracts electrons in a bond with force given by the electronegativity specific to that element, the electrons are pulled more or less in a particular direction, causing the charge in the bond to be distributed unequally among the atoms. As the dipole is relatively easy to measure, we can use it to calculate quantities like the interatomic distance (much harder to measure).

What is the dipole moment of two opposite charges of 0.5 C at 20 cm?

The dipole moment of two charges q and -q, with q = 0.5 C, separated by 20 cm, is p = q × d. To find this result:

Convert the distance to meters:

20 cm ≡ 0.2 m.
Multiply the charge by the distance:

q × d = 0.5 C × 0.2 m = 1 C · m

This is the dipole moment. Notice that, by definition, it points from the negative charge to the positive one (as it is a vector).