Percent Ionic Character Calculator

With our percent ionic character calculator, you will explore the polar nature of chemical bonds. In this article, you can learn the following:

• What is a chemical bond? The types of bonds and the relationship between covalent and ionic bonds.
• What is the percent ionic character of a bond — what's in the middle will be explained.
• How to calculate a bond's percent ionic character from the difference in electronegativity.
• How to calculate the percent ionic character from the dipole moment.
• And much more!

We must understand where and why we define this quantity to calculate the percent ionic character: let's talk chemical bonds. We identify three types of chemical bonds:

• Covalent bonds;
• Ionic bonds; and
• Metallic bonds.

The metallic bond is a bit on its own, so we neglect it in our article. Covalent and ionic bonds are "connections" between two different atoms. In covalent bonds, atoms share a specific number of electrons, completing their valence shells. Neither atom gets a larger share of the communal electrons. On the other hand, ionic bonds see one atom "ripping" one electron, or more, and completing their valence shell, while the other atoms reach the lower valence shell. Ionic bonds form between ions, too, neutralizing the charge of the atoms in the process.

In the process of reading this article, if you need a refresher on the concept, visit our electron configuration calculator.

You can see the difference between the covalent and the ionic bond if you consider the distribution of the shared charge between the two atoms. Evenly distributed charge defines covalent bonds, while atoms entirely hogging or discarding the shared charge represent ionic bonds.

Ionic and covalent bonds are not too far from each other. The differences we highlighted above are easily placed on a spectrum. On one side, we find pure covalent bonds, for example, bonds between two atoms of the same species. The shared charge is distributed equally among the two atoms in this case. We can't identify a dipole moment, and the overall system composed of the two atoms is non-polar. We can call this type of covalent bond non-polar covalent bond.

When atoms belong to different species, one will be "bossier" than the other, attracting a larger share of the communal electrons. This imparts a polar moment to the bond. We call this type of bond polar covalent bond. If the pull of one atom increases even more, we can reach a point where the shared electrons are entirely in possession of one of the atoms: the bond becomes purely ionic.

This progressive transformation of a covalent bond into an ionic bond defines the percent ionic character of a covalent bond.

Which quantity describes the tendency of an atom to attract the shared electrons in a stronger or weaker measure? Electronegativity. Electronegativity (denoted by the Greek letter $\chi$) is a property specific to each element that depends on two quantities:

• The atomic radius: electronegativity decreases with increasing atomic radius (descending in the columns — groups — of the periodic table).
• The nuclear charge: the higher the charge, the higher the electronegativity. This means that electronegativity increases from left to right in each row (period).

According to these rules, fluorine has the highest electronegativity, while cesium has the lowest. We also see that alkali and alkaline earth metals have the lowest electronegativity in the respective periods, while nonmetals tend to have higher electronegativities.

Electronegativity is measured with different scales, the one curated by Pauling being the most commonly used.

When two atoms with vastly different electronegativities bond, the one with the highest value will attract the shared electrons enough to impart a markedly ionic character to the bond. How do you find a bond's ionic character (in percent)?

Linus Pauling came up with a formula for the percent ionic character, as opposed to the previously used method involving the quantification of the dipole. In Pauling's formula for the percent ionic character, you must only know the difference in electronegativity between the atoms in a bond.

The formula is:

where:

• $I$ — Ionicity: the calculated percent ionic character of the bond; and
• $\Delta\chi = \chi_1-\chi_2$ — The difference of the electronegativities of the involved atoms.

Notice that the specific element in the bond doesn't matter: as long as the difference in electronegativity remains the same, the percent ionic character doesn't change.

The maximum value for $|\chi_1-\chi_2|$ equals the difference in electronegativity between fluorine and cesium: $3.98-0.79 = 3.19$. The minimum value is, of course, $0$.

Now that we know how to find the percent ionic character from the electronegativity, we can plot the function:

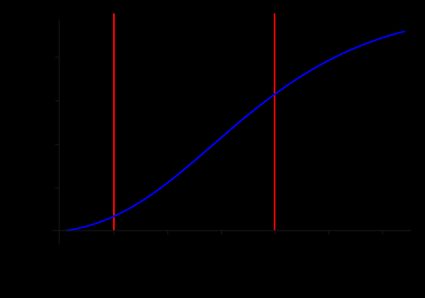
In this graph, we identify three regions, each associated with a specific bond behavior. Let's see them in a table:

You can also calculate the percent ionic character from the dipole moment. The formula in this case is:

where $\mu$ is the dipole moment. The calculated dipole moment assumes that the bond is entirely ionic. In this situation, we can calculate this quantity as follows:

where:

• $q$ — Charge shared in the ionic bond, measured in multiples of the charge of the electron;
• $e$ — Elementary charge of the electron, with $e = 1.602\times10^{-19}\ \mathrm{C}$; and
• $d$ — Bond length.

The result of these calculations is in coulomb meter, which, in chemistry, is often far too small to handle comfortably. The Debye, a measure of the electric dipole between equal charges with opposite sides at a distance $d = 1\ \text{\AA}$, is a much more reasonable measurement unit for the scope.

The conversion between Debye and Coulomb meters is as follows:

Let's take the molecule of the hydrogen fluoride, $\rm HF$. What is the character of the single bond between hydrogen and fluorine?

We start by finding the electronegativity of the two atoms:

• $\chi_\mathrm{H} = 2.20$
• $\chi_\mathrm{F} = 3.98$

Calculate now the difference in electronegativity (the sign doesn't matter):

The percentage of an ionic character calculated using Pauling's formula is:

Comparing the result with the table above suggests that the bond between hydrogen and fluorine is highly polar while still being covalent. The fluorine keeps the largest share of the common charge.

Here is another example, this time with the dipole moment: Let's consider another hydrogen compound: hydrogen iodide. In this case, we need to know:

• The bond length $d = 161\times10^{-12}\ \mathrm{m}$; and
• The measured dipole moment: $\mu_\mathrm{observed} = 0.44\ \mathrm{D}$.

We find the calculated dipole moment:

This dipole moment corresponds to $7.73\ \mathrm{D}$. We know how to find the percent ionic character:

According to the subdivision above, this bond is entirely covalent, with only slight traces of ionic behavior.

Our percent ionic character calculator implements both formulas used to compute this quantity, and we linked them, too!

To find the percent ionic character, simply insert the known data: the electronegativities for Pauling's formula or the dipoles. If you insert enough data, we can compute the remaining variables in both formulas at the same time!

If you are interested in the details of the science of chemical bonds, you can visit our bond order calculator.

The percent ionic character of a chemical bond is a measure of the shared charge distribution in a bond between two atoms. This quantity measures how much one of the atoms in the bond dominates in the sharing of electrons in the bond: the higher the percentage, the higher the ionic character.

To calculate the percent ionic character from the electronegativity, follow these easy steps:

1. Calculate the difference in electronegativity between the two atoms in the bond.
2. Divide by two the result, and take the square.
3. Raise e (the Euler number) to the exponent found in step 2, changed of sign.
4. Subtract the result from 1.
5. Multiply the result by 100.

The result is the percent ionic character of the bond.

The percent ionic character of the OH bond is 31.91%. To find this result:

1. Find the electronegativity of the two atoms:

   • Hydrogen has electronegativity χ_H =2.20; and

   • Oxygen has electronegativity χ_O = 3.44.

2. Find the difference between these values: Δχ = 3.44 − 2.20 = 1.24

3. Compute the Pauling's formula:

   I = 100 · (1 − e^{-0.25 · 1.24²}) = 31.91%

The OH bond is polar covalent.

Ionic and covalent bonds are chemical bonds where two and only two atoms share a defined number of electrons. However, in the covalent bond, the electrons are more balanced than in an ionic bond, where the atom with higher electronegativity keeps the shared electron entirely in its valence shell (effectively acquiring a negative charge). At room temperature, ionic compounds are more likely to be found in the solid state, while covalent ones are in liquid or gaseous form.