Compton Scattering Calculator

The Compton scattering calculator is a tool that helps you to find the wavelength extension of a photon scattered by any angle in this particular case.

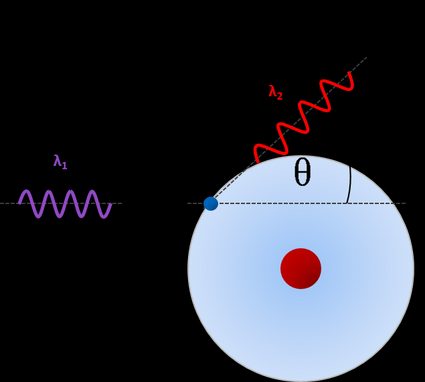
The Compton effect is among the possible interactions between light and matter. After this process, the wavelength of the photon increases, and the traveling direction changes. It is one of the phenomena which confirm the corpuscular nature of light.

A single photon can be treated as a massless particle that transports energy depending on its wavelength or frequency (you can quickly switch between these two using our wavelength calculator).

When a photon collides with another particle, let's say an electron, its propagating direction can change. We can describe the process as a classical elastic collision between two bodies, meaning that energy and momentum are conserved. If the electron is free or weakly bonded in the atom, we can assume that all of the initial energy comes from the incident photon. This assumption is well satisfied for X-rays, for which the Compton effect plays an important role.

We can determine the difference between the wavelengths of scattered and incident light with the Compton scattering equation:

where:

• $h = 6.62607 × 10^{-34}\ \rm J/s$ – Planck constant;
• $m$ – Mass of the particle;
• $c = 299\, 792\, 458\ \rm m/s$ is the speed of light; and
• $\theta$ – Angle between the directions of scattered and incident rays.

$h / (m\,c)$ is a Compton wavelength of the object which causes the scattering. You can find more information about this topic in Omni's Compton wavelength calculator.

We can easily find that the most significant extension of photon wavelength happens for $\theta = 180\degree$, which equals two Compton wavelengths, whereas, for $\theta = 0\degree$, there is no energy loss, which corresponds to no scattering process.

Let's calculate the wavelength extension of a photon scattered on the free electron by an angle $\small \theta = 80\degree$.

• Find the rest mass of electron: $\small m = 9.109 \times 10^{-31}\ \rm kg$;

• Estimate cosine of a given angle: $\small\cos(80\degree) = 0.174$;

• The Compton wavelength of an electron is:

• Work out a wavelength extension: $\small\Delta\lambda = 2.426\ {\rm pm} \times (1\! -\! 0.174) = 2.005\ \rm pm$.

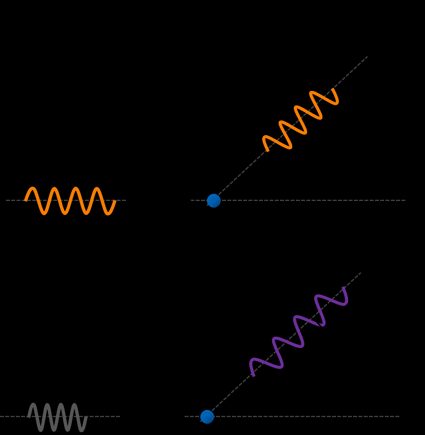
Now let's consider two photons of different initial energies: 2 eV and 20 keV, which correspond to red-orange light and so-called hard X-ray, respectively. We can easily find the values of wavelengths with photon energy calculator and equal about 620 nm and 62 pm.

You can estimate the wavelength extension as the percentages of initial wavelengths, which are 0.000323% and 3.23%, respectively. These results mean that Compton scattering is practically negligible for visible light, whereas for X-rays, a noticeable fraction of energy changes.