Car Center of Mass Calculator

The car center of mass calculator is a handy tool that estimates the location of an essential parameter of your car that you can't determine at first glance – the center of gravity. All you need is a car scale and computations implemented in our car center of gravity calculator.

In the following article, you will find step-by-step instructions on how to find the center of gravity of a car, the importance of this quantity (especially race car center of gravity), and the physics behind it.

The center of mass (or the center of gravity) has various definitions. Regarding vehicles, we can say that this is a unique point at which a car behaves as if all its mass were centered at that point. If you apply any force to this specific point, a vehicle will start to move in the direction of that force without rotating. To fully describe the center of mass of a three-dimensional object, you need to estimate three coordinates:

• Longitudinal position (determined by distances a and b);
• Altitudinal position (determined by height h); and
• Side position (determined by distances x and y).

Where these three coordinates intersect in space is the actual center of mass. Determination of the center of gravity consists of a few weight measurements of the car in different geometries.

Additionally, you need to measure such parameters as the wheelbase L (distance between the front and rear axles), the radius of the wheels r, and the height at which the wheels were raised H in case of altitudinal location, and the car track T in case of side location (distance between the wheels on the same axle).

Interested in physics applied to cars? Don't hesitate and check out our car crash calculator! We explain there how dangerous car crashes can be and how seatbelts protect you from injury.

To estimate the exact position of the center of gravity in your car, you need to perform a few measurements. In the center of mass calculator, we presented an idea of how to determine the center of mass in one, two, and three dimensions for two point masses. However, our car center of mass calculator is more complicated, so we have divided the step-by-step instruction into three parts:

Longitudinal position

1. Enter the weight of your car – for example, 3000 lb.

2. Find the wheelbase of your car – measure the distance between the centers of two wheels of different axles. Let's say it is 8 ft.

3. Ride up with the front (or rear) wheels on the scale and measure the weight of the front (or rear) axle. Remember that both axles should be on the same level! Therefore, you should place another axle on some platform of the same height as the scale. The measured mass should be approximately two times smaller than the total mass of a car. For example, we've got 1800 lb.

4. Read the resulting distances a and b, which determine the longitudinal position of the center of mass. In our example, a = 3.2 ft and b = 4.8 ft. It means that the car's center of gravity is slightly moved to the front. It is the most frequent situation because, in almost every car, the hefty engine is placed under the hood in the front.

Altitudinal location

1. Find the longitudinal position of the center of gravity of your car. You can, of course, use our car center of mass calculator to do it. In our example, we assume that we have the same car as before.

2. Decide which axle you will raise – front or rear. To find the height of the center of mass, you need to lift a little bit one of the axles (like in the figure above). For example, we have lifted the front axle.

3. Enter the height at which chosen axle was raised compared to the other axle. The higher you lift the wheels, the more accurate result you will get. However, be careful with doing this – protect your car from sliding from the scale! Always chock the wheels and use the parking brake. The height of 15 inches should be high enough, and this is a value we have used in our example.

4. Enter the radius of the car wheels. In practice, this is the distance from the wheel center (axle) to the ground. In our case, this is 12 inches.

5. Measure the weight of the front (or rear) axle. It doesn't matter whether you measure the weight of the raised wheels or the wheels on the ground. The raised axle should weigh slightly less than measured in the flat position of a car, and the axle on the ground should be a little heavier. In our example, let's say we have weighed the rear wheels and obtained 1440 lb.

6. Read the resulting height h, which is the height of the center of mass above the ground. In our case, we've got about h = 5 ft.

Side location

1. Enter the weight of your car – for example, 3000 lb.

2. Find the car track of your car – measure the distance between the centers of two wheels of the same axle. Let's say it is 4 ft.

3. Ride up with the left (or right) wheels on the scale and measure their weight. Remember that all four wheels should be on the same level! Therefore, you should place another two wheels on some platform of the same height as the scale. The measured mass should be approximately two times smaller than the total mass of a car. For example, we've got a weight of 1550 lb of the left wheels.

4. Read the resulting distances x and y, which determine the side position of the center of mass. In our example, x ≈ 1.93 ft and y ≈ 2.07 ft. Cars are usually symmetric in weight distribution in the front view, and the center of gravity will be approximately in the middle x ≈ y.

Before you begin your measurements: Be aware that all baggage (e.g., fire extinguisher) and people inside a car influence the center of mass. Make sure that your tire pressures are set right and that your car is tanked with fuel (if required). If you're doing measurements alone, you can use some weights that resemble your weight in the driver's seat.

The weight distribution is essential in vehicle handling. It defines the car's response to a driver's inputs and how it moves along the road. A race car's center of gravity is crucial in balance and steering.

The longitudinal position of the center of mass, related to the wheelbase, determines the load transfer between the front and rear wheels. The car will tilt respectively forward and backward during braking and acceleration. On the one hand, the vehicle with a much higher weight load on the rear axle tends to understeer – the car does not turn enough and leaves the road.

On the other hand, the vehicle turns more sharply than intended and could even get into a spin if there is a much greater weight load on the front axle. This situation is called oversteer. In the scheme below, the understeer is presented on the left and the oversteer on the right.

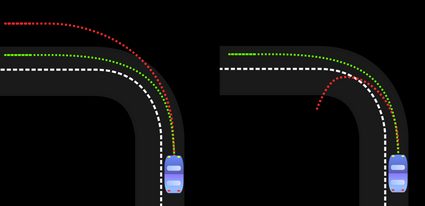
The altitudinal position of the center of mass, related to the car track, determines the load transfer from side to side. This parameter is important when cornering. The cars with a high altitudinal center of mass will more likely tilt on turning and may even topple. A lower race car's center of gravity is a principal performance advantage, especially compared to the SUVs. The car body of those sports cars is often made of lightweight materials to lower the center of gravity further. This is why Formula One cars are so low (their center of gravity is only about 10 inches high).

The center of gravity is also crucial in car stunts. You can learn more about it in our car jump distance calculator!

In the following section, we will try to explain how to derive all the necessary formulas for the car's center of mass. At equilibrium, the total force and, more importantly, the total torque acting on an object is equal to zero. This is a starting point for our considerations.

Longitudinal position

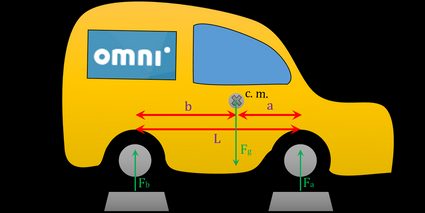
Let's suppose both car axles lie on the weighing scales, as in the figure above. According to Newton's 3rd law of motion, for every action, there is an equal and opposite reaction. That's why there are three forces: gravitational force Fg acting on the center of mass, reaction force Fb acting on the rear axle, and reaction force Fa acting on the front axle.

The total torque around any point should be equal to zero. As a reminder, the torque is a simple product of the force and arm length when the force and arm vector are perpendicular to each other (we described this physical quantity more in detail in the torque calculator). Let's sum up the torques around the rear axle:

Fb × 0 + Fa × L - Fg × b = 0,

and after a trivial transformation:

b = L × (Fa / Fg),

where Fa is actually the weight measured by the scale under the front axle. Similarly, we can sum up the torques around the front axle, and we will get the following:

a = L × (Fb / Fg),

where Fb is consequently the weight measured by the scale under the rear axle.

Altitudinal position

The calculations of the altitudinal position of the center of mass are a little more complicated, but the idea remains the same. Let's raise up the front axle. We want to sum up every torque around a certain point and equate it to zero. There are still three forces, but the two reaction forces are slightly different.

Let's take the summation of the torques around the front axle:

Fa' × 0 + Fb' × L×cosθ - Fg × |AC| = 0,

where Fa' and Fb' are weights measured by the scale under, respectively, the front and the rear axles. The length L×cosθ can be obtained directly from the figure above. The angle θ technically tells us how high we have raised one of the axles. Now, we only need to estimate the length |AC|. We can do it through a few observations:

1. There are three similar triangles with the angle θ. They are red in the figure above. The similar triangles calculator might be a handy tool for understanding this concept.

2. The distance |AB| = |DE| = (h - r) × sinθ, where h is the height of the center of mass, and r is the radius of a wheel.

3. The distance |BC| = |EC| × cosθ = a × cosθ, where a is the longitudinal position estimated previously.

4. Finally, the distance |AC| = |AB| + |BC| = (h - r) × sinθ + a × cosθ.

We can put the last result into the torques summation and after a few transformations:

h = [(Fb'/Fg)×L - a] × cot(θ) + r,

where cot(θ) is a cotangent function and the angle θ = asin(H/L) is an arcsine function. Eventually, we can rewrite it substituting a = L × (Fb / Fg):

h = (Fb' - Fb)/Fg × L × cot(θ) + r,

where Fb' - Fb is the weight change of the rear axle after raising the front wheels. We can realize a similar approach with the torque summation around the front axle:

h = (Fa - Fa')/Fg × L × cot(θ) + r,

and in that case, Fa - Fa' is the change of weight of the front axle after raising the front wheels.

Side position

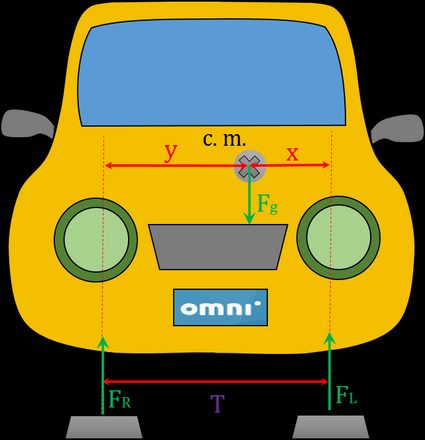
Calculating the side location of the center of mass is as simple as estimating the longitudinal position. Let's suppose the left wheels lie on one scale and the right wheels on another. There are three forces: gravitational force Fg acting on the center of mass, reaction force FL acting on both left wheels, and reaction force FR acting on both right wheels. Let's sum up the torques around the left wheels (actually around the center point between two left wheels):

FL × 0 + FR × T - Fg × x = 0,

and therefore:

x = T × (FR / Fg).

Similarly, with the right wheels:

y = T × (FL / Fg).

Now you know how to find the center of gravity of a car. Our car center of mass calculator uses all the above equations and thus simplifies calculations. Just use our tool and find out how quickly it works!