Car Jump Distance Calculator
The car jump distance calculator is here to help you simulate the very dangerous but, for sure, phenomenal stunt – jumping in the car from one ramp to another. Remember that we should consider many different factors during a car jump, but we can't take them all into account.
Even if it isn't 100% accurate, the car jump distance calculator still allows you to estimate the expected jumping range and landing angle including the air drag force. These are crucial parameters and should be known before any trial jumps.
Keep reading to learn more about the calculator and physics behind the car jumping problem!
How to use the car jump distance calculator?
We divided the calculator into three parts.
Basic jump parameters
That's the central part which is obligatory to see any results. You need to provide:
- Take-off ramp slope and height – the slope should be expressed in angle units;
- Landing ramp height – note that we show the results for only first part of the jump if the landing ramp is too high for a jumping car;
- Take-off speed – the speed that the car has just before take-off; and
- Standard gravity – by default, we set it to , which is the mean gravitational force on Earth. You can adjust it to the standard gravity at your location or change to standard gravity of other planets.
That's enough to analyze a simple projectile motion problem. For more advanced computations, you need to input more values. Decide whether you want to include the air drag force, compute car tilt during a jump, or both. A new section called "Advanced calculations" should appear.
Advanced calculations
Regardless of what advanced options you choose, you need to specify car mass, length, and height. The former is the total mass of a car including all equipment, fuel, and the passengers' weight. Additionally, the air drag force option requires:
- Air density – which for standard conditions is . Use our air density calculator to find the density of air for your specific jumping conditions; and
- Automobile drag coefficient – you can check the drag coefficient for various cars, e.g., .
The car tilt computation needs the following additional parameters:
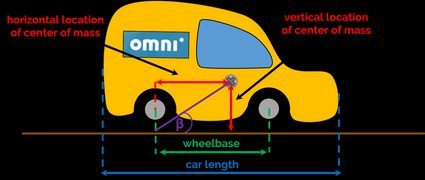
- Wheelbase – the distance between car's rear and front axles;
- Horizontal and vertical locations of the center of mass – in other words, the longitudinal and altitudinal positions (see the picture that should appear in the calculator), which you can estimate using our car center of mass calculator;
- Car height – the car height is required to approximate the moment of inertia (if you don't know its value) and air resistance; and
- Moment of inertia – if you know the exact value of the moment of inertia, you can input it directly in the corresponding field. This moment of inertia is around the axis passing through the car's center of mass and parallel to the car's width (the calculator will move the axis of rotation to the correct place automatically). Read the FAQ below to learn how we find the approximation of mass moment of inertia in the car jump distance calculator.
Results
The results section consists of:
- Summary table – includes the most interesting car jumping parameters like range, time of flight or landing tilt angle; and
- Customized chart – specify what should be on the x-axis (horizontal position or time) and y-axis (position, velocity, acceleration, or car tilt angle). You can add up to three graphs at the same time.
Move down the calculator to change the quantities and their units appearing in the table or chart.
Determination of the distance traveled mid-air
You can treat the launching of a car from a ramp as a projectile motion with an initial velocity and angle of launch . The standard way to analyze a projectile motion trajectory is to treat the horizontal and vertical positions as separate variables. We'll use differential equations, which is a suitable method to deal with more complex problems (e.g., including drag force). If you want a simpler approach, visit our projectile motion calculator.
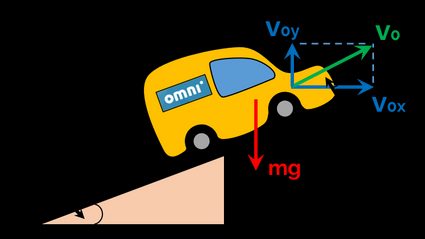
The only force acting upon the car is the gravitational force, equal to the mass multiplied by the standard gravity . Furthermore, we can decompose the velocity vector into two perpendicular vectors using the sine and cosine trigonometric functions. The first component is in the horizontal direction and the second one in the vertical direction . The two sets of differential equations are then:
with initial conditions:
where stands for initial height and for time since take-off. We'll skip the whole procedure, but it shouldn't be hard to find the solution for a person who is familiar with differential equations:
Just for the sake of completeness, we listed some of the most interesting parameters that you can derive from the above equations.
Velocities
Accelerations
Maximum height and associated time
Time of flight and range
In the latter case, we have introduced the height of the landing ramp to have a more general result.
Car jump with air drag force
Let's introduce the air resistance into the computations of car jump trajectory. We'll use the most common form of the drag formula we described in the drag equation calculator:
where:
- – drag force;
- – air resistance coefficient; and
- – car velocity.
The air resistance coefficient is equal to:
where:
- – air density;
- – cross-sectional area of the car, seen from the movement direction; and
- – drag coefficient that depends on the shape of the moving object.
The drag equation consists of several variables, which we often treat as constants for simplicity. However, it isn't true in general. The car rotates mid-air, meaning that the cross-sectional area and drag coefficient generally change their values during the jump. That drastically complicates the problem, and to find the exact solution, you might have to use numerical simulations we cannot provide.
Still, in the car jump distance calculator, we assumed that b is constant, which is approximately the case if a car doesn't rotate very much. So, let's write the same differential equations as before but extended by air resistance contribution:
The symbol means that there is for the car rising and for the car falling. The initial conditions remain the same as in the previous section, except for two additional conditions:
The solution for variable is in the relatively simple form with natural logarithm:
The vertical position time-dependence has a much more elaborate set of formulae involving the inverse cosine and hyperbolic cosine functions:
when a car is rising:
when a car is falling:
where we used the following and coefficients under the square root:
As you can see, to evaluate the vertical position while falling, you need to know the maximum height and associated time . We'll give the appropriate formula later, but let's focus on other parameters to keep the previous order.
Velocities
when a car is rising:
when a car is falling:
where we used tangent function, and hyperbolic tangent function.
Accelerations
when a car is rising:
when a car is falling:
Maximum height and associated time
Time of flight and range
where we used the inverse function of the hyperbolic cosine.
That's it! Quite tedious, isn't it? You can try to input the results into the starting differential equations to verify the answer. Furthermore, it's a good idea to investigate the limits of and at zeros. Will they lead to the projectile motion without air resistance? 🤔
Why is a car tilting during the jump?
If you have ever seen a car launching from a ramp (or any other inclined plane), you have surely noticed that the . The main reason for this lies in the non-zero take-off time. The front axle of the car losses contact with the ramp first, and then, after a fraction of a second, the rear axle. Even if that short, this amount of time is enough to put the car into rotation.
To understand the , we have to consider a car as a rotating rigid body. There are two phases of rotation:
- Angular acceleration – only the rear axle touches the ground. In this phase, the car starts to rotate, gaining a certain angular acceleration value until the rear axle take-off the ramp.
- Constant angular acceleration – when all the tires are mid-air, the car rotates with constant angular acceleration until landing.
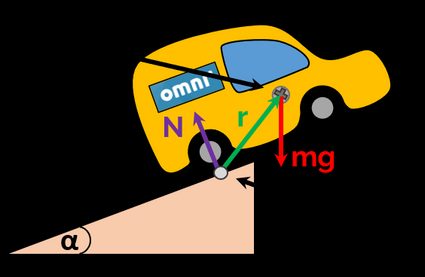
Let's focus on the first phase. The axis of rotation goes through two points located on the bottom-most part of the two rear tires, as in the picture above. The car is subjected to the two forces: a gravitational force acting on the car's center of mass and ground reaction force originating from the tire-ground interface.
Since we need to calculate torque , we can omit the latter force in the further analysis (it acts on the points localized at the axis of rotation). Ultimately, we can use torque to calculate the angular acceleration and final angular velocity , which is all we need to know to proceed to the next phase.
The last phase is a much simpler problem because there is no torque mid-air. Therefore, angular acceleration vanishes and angular velocity has a constant value. Eventually, that allows us to calculate the landing angle by multiplying the angular velocity with the time of flight, or more precisely, the duration of the last phase.
Knowing the final tilt angle is crucial to make sure the landing is safe. You will always want to land on the car wheels (front, rear, or preferably both axles) and not hit the ground with the hood or the rear bumper. Guerlain Chicherit is a French rally driver who that ended up in the car crash because of a wrongly predicted tilt angle. Thankfully, he wore a seatbelt! Check the car crash calculator to see the importance of using seatbelts.
How fast does a car rotate?
After learning about the principle of car jump rotation, let's dive deeper and see how we can describe the rotational movement with physics. Using the physical quantities we saw in the previous section, we arrive at the following differential equation:
where:
- – mass moment of inertia of the car around the axis of rotation we defined earlier.
- – angular acceleration vector we have written as the time second derivative of car angle in regard to horizontal level. Negative means that car's front starts to point upwards, and positive the other way around – the car's front starts to point downwards.
- – torque vector that equals only its second term, the cross product of the position vector from the axis of rotation to the center of mass, and gravitational force vector ( – car mass). The first term of equals zero because the position vector is zero as well (ground reaction force is applied at the axis of rotation).
Let's simplify the equation by switching from vectors to magnitudes only. We can do this using the sine function:
where is the angle between and vectors. For and , the angle is:
where is the angle created by the position vector and the car's horizontal plane. The is basically 90° expressed in radian units.
Because there is term in the formula, it is convenient to switch from sine to cosine, leaving in the argument and with additional minus before everything. Tying it all up, we arrive at the following equation:
which we need to solve with the following initial conditions:
The first condition says the car's initial tilt angle is the launching ramp angle , and the second states that the car is not rotating before launching.
Unfortunately, it is not possible to find a simple analytical solution to that equation. In general, you need to use numerical methods to solve it for a particular case (we do it in the car jump distance calculator). However, if the car moves fast enough, you can assume that won't change during the launching phase meaning that angular acceleration is constant:
So, there are no differential equations involved. The sign of computed determines the rotation direction. For the car's front starts tilting towards the ground and for the car's front starts to tilt towards the sky.
The last thing to consider is how to find the angle for a certain car. It requires determining the horizontal and vertical positions of the center of mass in the car. To calculate , you need to use the inverse tangent function:
where:
- – the altitudinal center of mass position, the vertical distance measured from the ground to the center of mass; and
- – the longitudinal center of mass position, the horizontal distance measured from the rear axle to the center of mass.
Similarly, you can calculate , but this time using the Pythagorean theorem:
How to calculate car landing angle?
From the previous section, you should know how to calculate angular acceleration of the tilting car, and you can do it numerically or make a high-velocity approximation. It's time to estimate the angle about which the car will rotate before landing. As before, there are two phases:
- Launching phase
It's the time passed between the car's front axle take-off to the rear axle take-off. The launching phase duration equals the wheelbase divided by take-off velocity :
If you decide to calculate numerically, you obtain the final angular velocity and take-off tilt angle along the way doing the computations for time . For the high-velocity approximation, we obtain:
- Mid-air phase
The rest of the jump proceeds with constant angular velocity meaning the rotation angle during this phase equals , where is the time of flight.
Eventually, the landing angle we find in the car jump distance calculator is the sum of the above two angles and the initial ramp angle :
Car stunts in movies and real world
Car jumps are present in many action movies where the moment when a car takes-off from the ramp is one of the most spectacular parts of the entire film. For example, there is a in which Nicolas Cage jumps over the long waiting traffic on the bridge in his Ford Mustang Shelby GT500. Car jumping scenes are often performed more than once to catch the best shot, so nowadays, these scenes are instead computer-generated.
Still, some stuntmen perform real-life car jumps. Here are some examples:
- Travis Pastrana jumped 269 ft (82 m) over the river at the Long Beach (California) in 2009 ()
- Tanner Foust jumped 332 ft (101 m) from the Hot Wheels ramp in Indianapolis 500 in 2011 ()
- Bryce Menzies jumped 379 ft (116 m) over New Mexico ghost town in 2016 ()
As a bonus, check out the film featuring Travis Pastrana and his . The show begins with a car jump giving a spectacular performance!
FAQs
What should I know before jumping with a car from a ramp?
First of all, despite all our efforts, we cannot perform exact calculations, which would require modeling a particular car and specific jumping conditions.
Before deciding to make a big jump, do some tests with small launching angles and gradually increase the ramp angle. Also, note that a car would most probably slow down on the ramp resulting in lower jumping ranges. You don't want to hit the edge of the ramp with your hood!
What does car tilt angle mean?
The car is rotating mid-air because of the instantaneous torque acting on the car's center of mass. When the angle is zero, then the car is oriented parallel to the horizontal axis. For negative angles, the car front points up, and for positive angles, the car front points down.
It's a standard way to measure the angle in polar coordinates. The zero is along the x-axis to the right, 90° is along the y-axis upwards, and so on.
What do the distance, total speed, and total acceleration mean?
The chart we're showing in the car jump distance calculator allows you to choose one of the physical parameters that change during the jump. The quantities with x and y subscripts should be clear – they are positions, velocities, and accelerations measured in a particular direction. The meaning of the remaining parameters without subscripts are the following:
- Distance d – the distance from the launching point calculated as d = √(x2 + y2);
- Total velocity |v| – the speed of the car calculated as |v| = √(vx2 + vy2);
- Total acceleration |a| – the total acceleration of the car calculated as |a| = √(ax2 + ay2); and
- Tilt angle θ – the angle of the car in respect to the horizontal line.
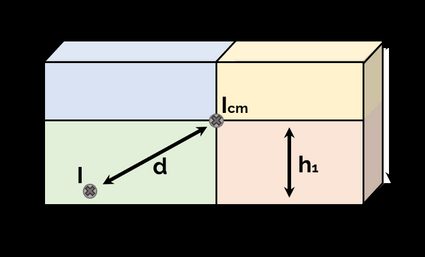
How to approximate the car's moment of inertia?
In our calculator, we model the car as a solid rectangular prism of constant density with an axis of rotation passing through one of its sides (width). To achieve that, we start with the following for the solid cuboid moment on inertia:
Icm = 1/12 * m * (l2 + h2)
where:
- Icm – the moment of inertia of solid cuboid rotating about an axis passing through the center of mass parallel to the width of the cuboid;
- m – mass;
- l – cuboid length; and
- h – cuboid height.
However, the center of mass of the car does not lie in the center of the cuboid, so the formula must be revised. We did it by calculating and summing up four smaller cuboid boxes moments of inertia, which eventually leads to the following formula:
Icm = 1/3 * m * [h2 + l2 - 3 * h1 * (h - h1) - 3 * l1 * (l - l1)]
where h1 and l1 are the height and length that determine the position of the center of mass (check the first section for a picture).
Finally, to move the axis of rotation passing through the center of mass to the actual axis of rotation, we use the parallel axis theorem:
I = Icm + m * d2
where I is the moment of inertia about the axis parallel to the first axis and displaced from it by distance d.
