Center of Mass Calculator

With this center of mass calculator, you can quickly find out the center of mass of up to 10 discrete masses. What is more, the tool allows you to choose between 1-, 2- or 3-dimensional systems. Impressive, isn't it? Below you'll also find the center of mass definition, as well as information on how to find the center of mass of a triangle.

Apart from the physics lesson, the center of the mass equation may be useful in real-life applications:

• If you're wondering how to find the center of mass when swinging with your child on the seesaw, you can make quick calculations with our tool;
• For the DIY enthusiast, the center of mass equation is super useful for making, e.g., a crib or ceiling mobile; and
• For those interested in cars, we also have the unique car mass center calculator!

The center of mass is the point at which the whole mass of the body or system can be considered to be concentrated. In other words, if you apply a force to that point, it will cause only linear acceleration and no angular acceleration. Don't forget that if the object has uniform density, then the center of mass is located at the centroid of the object. This fact can make your calculations way easier!

In one plane, you can imagine the center of mass as a lever or a seesaw, with a mass on each end:

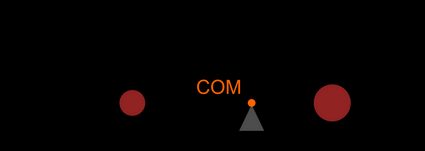
If you have two objects with the same mass, the center of mass will be exactly half of the distance between them. But what happens if you have a more massive object at one end? Where's the pivot point? Intuitively, we know that the center of mass will be closer to a heavier object. Where exactly it lays, you can find out using the center of mass equation.

In this center of mass calculator, the center of mass equation we've used is:

Center of mass = (m₁r₁ + m₂r₂ + ... + m_Nr_N) / (m₁ + m₂ + ... + m_N)

where

N - number of masses m

r_i - distance from the reference point

The center of mass equation can also be shortened to:

Center of mass = 1/M × Σ m_ir_i

where M is the sum of the masses of all of the particles: M = m₁ + m₂ + ... + m_N

That's the general formula, but you can also extend that center of the mass equation to 1,2, or 3 dimensions in the Cartesian coordinate system. For example, if you have N particles (up to 10 in our calculator) in 3D, you can calculate the center of mass using:

x_com = 1/M × Σ m_ix_i

y_com = 1/M × Σ m_iy_i

z_com = 1/M × Σ m_iz_i

where i = 1,2, ..., N.

The formulas above work perfectly for discrete masses. However, if you have a continuous object with variable density, the computation of its integrals is needed.

If you're searching for the center of mass of a triangle, we're pretty sure that you want to find the centroid of a triangle – the centroid of an object with uniform density. All you need to do is to calculate the arithmetic mean of the vertex coordinates. Given A = (x₁,y₁), B = (x₂,y₂), C = (x₃,y₃), the center of mass equation can be written as:

G = [ (x₁+x₂+x₃)/3 , (y₁+y₂+y₃)/3 ]

To calculate the center of mass of a triangle with this tool, enter the coordinates of the points of the triangle and make sure that the masses are all the same (the specific mass value doesn't matter). Also, you can simply use our centroid calculator.

While that is the most often common case, we cannot exclude the other cases: what happens if you have three masses forming the vertices of a triangle, but they differ in mass?

Let's assume that the mass in point B is 3 times bigger than the mass in points A and C:

As you can see, the center of mass moved towards the heavier point.

Center of mass and the center of gravity are the same when the gravitational field is considered to be uniform. So, if the gravity gradient effects are negligible (which is most cases), you can use both terms interchangeably. However, if you're looking at some large interstellar object, e.g., satellites and planets, a slight variation in the gravitational field may lead to torque, which would mean you need to differentiate between those two terms.

You can calculate the center of mass of a triangle in three steps:

1. Determine the x-coordinates, x₁, x₂, x₃.

2. Determine the y-coordinates, y₁, y₂, y₃.

3. Apply the center of mass formula:

   G = [ (x₁+x₂+x₃)/3 , (y₁+y₂+y₃)/3 ]

Assuming that the two objects are 50 cm apart, the center of mass of these two objects will be 25 cm from each object.

Since the masses are identical, the center of mass will be half the distance between them.

Understanding the center of mass is crucial for various fields, such as physics, engineering, and astronomy. It helps in predicting how objects will move or react under different conditions, such as when forces are applied.

The centroid is a geometric property and depends only on the object's shape, whereas the center of mass considers both shape and mass distribution.