Magnification of a Lens Calculator

Our lens magnification calculator will focus on the world of lenses in photography, finally explaining what magnification is, why it is different from zoom, and much more!

Here you will learn:

• The basics of optics, lenses, and images;
• What is the magnification of a lens?
• How to calculate the magnification of a lens – the magnification formula;
• An example involving kangaroos; and
• When do we need extender tubes?

And that's not all – magnify your knowledge with Omni Calculator!

A camera is nothing but lenses and a sensor. At least in theory! To understand how it works, we need to explore the world of optics.

A lens is a device made of a material with a different refraction index to air (there can even be electromagnetic lenses that act on electric currents). This and its shape allows it to bend rays of light as they come into contact with it.

Lenses can focus or "unfocus" light rays. In this tool, we will only consider converging lenses. Their main feature is the ability to focus every ray entering the lens parallel to the optical axis at a specific point, the focus.

The distance between the focus and the lens is the focal length $f$.

The diagram below will help explain the operating principles of a lens:

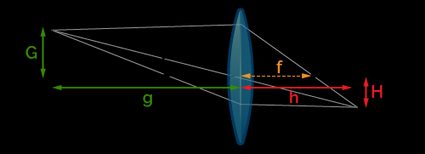
First thing – the upward facing arrow on the left of the image is the object we are looking at. The rays of light coming from it hit the lens. The one parallel to the optic axis (the topmost line) gets focused and so converges on the focus. The ray passing through the center of the lens meets the focused ray on the other side of the lens, which creates a flipped image called the real image of the object.

We can easily identify the main elements that we need in the description of a lens:

• The focal length $f$; and
• The focus distance $d$, given by $d=g+h$; we can, in turn, identify:
  • The distance between the real image and the lens, $h$; and
  • The distance between the object and the lens, $g$.

The distance $h$ is where the image is focused, thus where it can be observed with maximum sharpness.

The magnification of a lens is an absolute measure of how much the height of a real image differs from the object's height. Remember, that in a camera, the real image forms on the sensor (or on the film, if you're old school).

Now consider that the sensor is at most a few centimeters wide, while you can take a picture of the Eiffel Tower, which is $330\ \text{m}$ tall. Even from afar and with a powerful telephoto lens, you'll always get a magnification that is much smaller than you expect when taking pictures with a camera.

The formula for the magnification of a lens is:

Thanks to the properties of similar triangles, we can compute the magnification of a lens also using the distances between the object/image and the lens:

This allows you to adjust $h$ by slightly moving the lens — an action you did many times before taking the picture.

We can shuffle the equations a little to find a magnification formula that uses focal length and object distance:

$r$ is the square root of the following quadratic equation:

If you'd like to know more, try our others optic calculators dedicated to lenses, like the thin lens equation calculator or the lens maker equation calculator.

When you are snapping a picture, you don't usually know the values of $h$ and $g$, but you know the focal length for sure, and you likely know the distance between you and your subject. These two quantities are enough for you to calculate the magnification of your lens!

Imagine you are taking a picture of a huge kangaroo, let's say two meters tall and weighing $95\ \text{kg}$, like the one that terrorized Brisbane a few years ago.

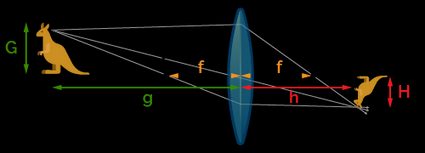
Since that beast would be too dangerous to photograph at a close distance, we suggest you use a $500\ \text{mm}$ telephoto lens. We advise you to keep your distance, let's say 150 meters (but remember that a kangaroo can reach a maximum speed of $70\ \text{m/s}$). Insert these values into our magnification of a lens calculator, which will return:

See? The value is way smaller than $1$. However (trust us), that kangaroo would look larger than life in the picture.

The values of $h$ and $g$ are hidden in the further magnification properties section of our calculator, so if you need to know either of these, just click the button!

Magnifying glasses are perfect for explaining the principles of magnification (the clue is in the name).

Their lenses are usually manufactured with a focal length of $25\ \text{cm}$. If you use the lens to look at an object closer to it than that distance, you create a virtual image of the object.

Do you remember the diagram we showed you already? We need to modify it slightly!

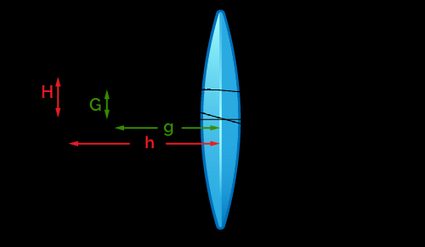
As you can see, now the rays on the right side of the lens do not converge. We are dealing in terms of virtual images, which originate from the virtual continuations of the rays, creating a non reversed image of the object.

If you consider the lens magnification formula using the heights of the image and the object:

The result is straightforwardly larger than $1$: a proper magnifier!

How do you increase the magnification of a lens? Well, there are only two options:

• Decrease the distance $g$ between the camera and your subject; or
• Increase the distance $h$ between the lens and the sensor.

In the case of violent kangaroos, it may be better to go for the second option: that's why camera manufacturers sell extension tubes, short rings to mount between the lens and the body, which end up increasing $h$ by some precious millimeters.

Expand the further magnification properties section to see the variable extension tube. We set it at $0\ \text{mm}$ by default, but change it according to your needs!

Maybe you expected the magnification to be a bigger number, something like $10\times$ or $20\times$, like the values you see on binoculars or telescopes (we made an entire calculator for that, check out our telescope magnification calculator).

However, when talking cameras, the magnification is usually a really small number. The number followed by a $\times$ is the zoom.

The zoom describes how much the lens's focal length can change by (there are such things as zoom lenses). A typical $18/55$ lens will have its zoom defined by:

We hope that the distinction is clear!

Are you still looking for photography-related calculators? Check out our shutter speed calculator.