Last updated: Apr 15, 2024

Duty Cycle Calculator

Q: What is the duty cycle of a pulsed radar that is on for 10 ms every second?

The duty cycle of such a system is D = 1% . You calculate it with the duty cycle formula: D = PW/D × 100% = 10 ms/1000 ms × 100% = 1% Remember to use the same units for all quantities. If our radar has a peak power of 20 kW , we can find the average power of the pulse is 200 W . Read more

Q: What does it mean to have a duty cycle of 30%?

A duty cycle of 30% corresponds to a system staying on for 30% of the period: our output would be high for about a third of a second every second. We used this formula: D = PW/T × 100% , where: PW — Pulse width; and T — Period. Alternatively, we can think of this system as a way to deliver an average power corresponding to a third of the peak power in the period: Pavg = 0.3 × Pp , where: Pavg — Average power; and Pp — Peak power. Read more

Table of contents

What is the duty cycle?How do I calculate the duty cycle from the pulse width?Why is the duty cycle useful?Examples of calculating the duty cycle FAQs

With Omni's duty cycle calculator, you can quickly find the value of this important quantity in many fields, from electronics to engineering. Keep reading this short but exhaustive article to learn:

What is the duty cycle?
How to calculate the duty cycle from the pulse width.
What is the relationship between the power and duty cycle?
Examples of duty cycle in real-world situations.

What are you waiting for? Omni's duty cycle calculator is here for all your needs!

What is the duty cycle?

The duty cycle is a measure of the fraction of time a periodic phenomenon (a signal, a mechanical part movement or process, you name it!) is "on", regardless of the effective intensity of the "on" part.

OK, maybe it's time to introduce some jargon; it will make things easier to understand! First, we talked of periodic phenomena: this means that they repeat cyclically in time. The time in which the phenomena repeats is the period.

We define the duty cycle in signals where, in a period, the power is on only for a certain fraction of the time, a pulse if you want. The time the pulse is on is the pulse width. We have all the ingredients to calculate the duty cycle, and we can now introduce the duty cycle formula.

How do I calculate the duty cycle from the pulse width?

The formula to calculate the duty cycle is:

D = \frac{PW}{T}\times 100\%,

where:

$D$ — Duty cycle;
$PW$ — Pulse width; and
$T$ — Period.

Notice that we measure both $PW$ and $T$ in time units, which makes the duty cycle dimensionless.

🔎 Why are we using a percent symbol? Because we are dealing with portions of a unit, expressing the duty cycle as a percentage gives us a quick idea of the width of the pulse.

We can also calculate the duty factor, which is nothing but the duty cycle, but expressed as a fraction of the unit rather than as a percentage:

d_\mathrm{f} = \frac{PW}{T}

This value is always smaller than one.

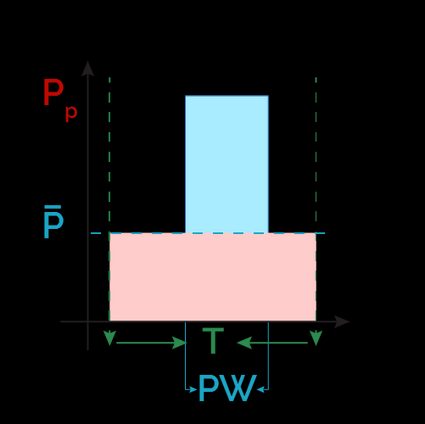
You now know how to calculate the duty cycle from the pulse width; what if we told you that there is a formula to calculate the duty cycle from the power of the pulse?

We need two quantities:

The power of the pulse, $P_\text{p}$ ; and
The average power in the period: $\overline{P}$ .

The formula is surprisingly similar to the one we met before:

D = \frac{\overline{P}}{P_{\text{p}}}\times 100\%

The average power in the duty cycle — Believe it or not, but the two rectangles have the same area: the duty cycle is the same!

🙋 Visit the watt-hour calculator to understand the relationship between time, energy, and power in depth!

Now that we have explained the calculations for the duty cycle, we can add one last formula that you can use to calculate the energy contained by the pulse. To do so, consider the dimension of energy:

\mathrm{Energy} = \mathrm{Power}\times\mathrm{Time}

Where can we find these quantities? We use a bit of common sense and choose the right pair of values. The energy of the pulse is:

E_{\mathrm{p}} = P_{\mathrm{p}}\times PW

By equating the two formulas we used to compute the duty cycle, we can find the analog expression:

E_{\mathrm{p}} = \overline{P}\times T,

🙋 To see the energy of the pulse in Omni's duty cycle calculator, click on advanced mode!

Why is the duty cycle useful?

The duty cycle is a valuable measure of the time a system will be used or available. Whether you know it or not, duty cycles appear in many situations in their "original" form (percentage of the period). You can meet one of them at Omni's 555 timer calculator.

Welders use the duty cycle to understand how long you can use a tool before it overheats, and you can apply the same concept to air compressors: the duty cycle is the time the compressor is on.

In networking, the uptime is a similar concept to the duty cycle: our uptime calculator will be even easier to understand after meeting the duty cycle calculator!

However, we need to go a bit deeper to see one of the most intriguing applications of the duty cycle: calculate the PWM, or pulse width modulation.

Here's a question: how do you obtain a sine curve using just a switch? Answer: with a dextrous use of the duty cycle. If you increase and properly decrease the duty cycle, the average power delivered to the circuit can approximate any arbitrary function.

In the picture below, you can see how varying the duty cycle (the light blue areas correspond to "on" fractions of the period) leads to a variation in the average power (the red line). We start with a small duty cycle (low average power), and we quickly increase the fraction of the time the system is on: $0.0$ , $0.1$ , $0.2$ , $0.3$ . The entity of the variations quickly reduces, and our curve flexes.

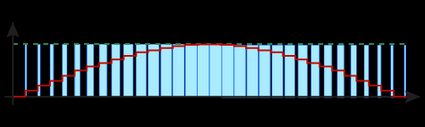
You can clearly see the sine function appearing from an on-and-off system! Obviously, the shorter the period, the better the approximation.

Examples of calculating the duty cycle

Take a classic NE555 circuit, and set its oscillation period to $T = 1\ \mathrm{s}$ . Now, choose the adequate component to set the high part of the output to $225\ \mathrm{ms} = 0.225\ \mathrm{s}$ . The duty cycle we calculate in this example is:

D = \frac{0.225\ \mathrm{s}}{1\ \mathrm{s}}\times100\% = 22.5\%

We can also calculate the duty cycle in the PWM examples above, maybe just the first steps. By calculating the sine function at an interval of $0.1$ , we find:

$\boldsymbol{x}$	$\boldsymbol{\sin(x)}$
$0$	$0$
$0.1$	$0.0998$
$0.2$	$0.1987$
$0.3$	$0.2955$
$0.4$	$0.3894$

The values of the samples are our desired average powers ( $\overline{P}$ ), normalized over the peak power. These values correspond to the duty cycle for each period. If our system has a period of $0.005\ \mathrm{s}$ , we can quickly find the times we must keep the signal "on". We apply multiple times the following formula:

PW = D\times T = D\times 0.005\ \mathrm{s}

$\boldsymbol{D}$	$\boldsymbol{PW}$
$0$	$0$
$0.0998$	$4.99\times 10^{-4}\ \mathrm{s}$
$0.1987$	$9.94\times 10^{-4}\ \mathrm{s}$
$0.2955$	$1.48\times 10^{-3}\ \mathrm{s}$
$0.3894$	$1.95\times 10^{-3}\ \mathrm{s}$

FAQs

What is the duty cycle?

The duty cycle is the fraction of the time a discrete periodic system is "on" in each period. We often express duty cycles as percentages: a duty cycle of 50% corresponds to a system in the "on" state half the time.

We can also relate the duty cycle to the system's peak and average power delivered.

How do I calculate the duty cycle from the pulse width?

To calculate the duty cycle from the pulse width, follow these steps:

Measure the period of the system T.
Take the pulse width PW, the time the system is on.
Make sure both quantities have the same units.
Calculate the ratio with the formula:

df = PW/T

This is the duty factor.
If you desire to find the duty cycle as a percentage, multiply the duty factor by 100:

D = df × 100%

What is the duty cycle of a pulsed radar that is on for 10 ms every second?

The duty cycle of such a system is D = 1%. You calculate it with the duty cycle formula:

D = PW/D × 100% = 10 ms/1000 ms × 100% = 1%

Remember to use the same units for all quantities.

If our radar has a peak power of 20 kW, we can find the average power of the pulse is 200 W.

What does it mean to have a duty cycle of 30%?

A duty cycle of 30% corresponds to a system staying on for 30% of the period: our output would be high for about a third of a second every second. We used this formula:

D = PW/T × 100%,

where:

PW — Pulse width; and
T — Period.

Alternatively, we can think of this system as a way to deliver an average power corresponding to a third of the peak power in the period:

Pavg = 0.3 × Pp,

where:

Pavg — Average power; and
Pp — Peak power.

Find the duty cycle

Pulse width (PW)

Period (T)

Results

Duty cycle (D)

Duty factor (df)

Pulse energy (E)

Check out 32 similar tech and electronics calculators 💻

3D printing costAmdahl's lawBattery capacity...29 more