Triangle Vertices Calculator
Are you looking to learn how to calculate the vertices of a triangle for math? Do you have a triangle for which you would like to find the vertices? If you answered yes to either of these questions, you are in the right place.
Our triangle vertices calculator will help you find the coordinates of the vertices using the coordinates of the midpoints.
Keep reading to learn:
- What is the vertex of a triangle;
- How to use our triangle vertices calculator; and
- How to find the vertices of a triangle using midpoints.
What are the vertices of a triangle?
The point at which two sides of a triangle meet is called a vertex. The word used to refer to more than one vertex is vertices.
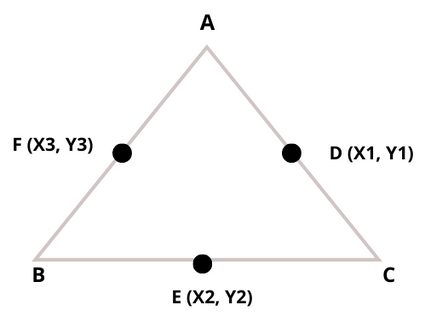
Instructions on how to use our triangle vertices calculator
To find the triangle's vertices , , and , you need to insert the and coordinates of the midpoints , , and , and our calculator will generate the coordinates of the vertices in real-time.
How to find the vertices of a triangle – vertices of a triangle formula
Let's look at the following problem.
A triangle has vertices , , and . The midpoints of the sides labeled , , and are (), (), and (), respectively. How do we go about finding the vertices using these midpoints?
-
Understand that: is (), is (), and is ().
-
Using the midpoint formula, find vertex :
Substitute in the values:
- Find vertex :
Substitute in the values:
- Find vertex :
Substitute in the values:
FAQs
How many sides and vertices does a triangle have?
Three. A triangle has three sides and three vertices. The vertices are the points where the three sides of the triangle meet.
How do I find the vertices of a triangle using the midpoints?
To find the vertices of a triangle using the midpoints, we use the following steps:
-
Identify the x and y values of the midpoints.
-
Use the midpoint formula:
A = (x₁+x₃-x₂, y₁+y₃-y₂)
B = (x₁+x₂-x₃, y₁+y₂-y₃)
C = (x₂+x₃-x₁, y₂+y₃-y₁)
-
Substitute in the respective x and y values.
-
Calculate the vertices of the triangle given by points A, B, and C.