Isosceles Right Triangle Calculator

Do you need an isosceles right triangle calculator? Do you need to find the area, perimeter, or lengths of the sides of an isosceles right triangle? This isosceles right triangle calculator will help you to do that and more. Keep reading to learn:

• What is an isosceles right triangle;
• How to use our isosceles right triangle calculator;
• How to find the perimeter of a right isosceles triangle;
• How to find the area of an isosceles right triangle;
• What a right isosceles triangle looks like; and
• How to construct an isosceles right triangle.

To use our isosceles right triangle calculator, enter the value of the known side in the correct field, and the lengths of the other sides, as well as the area and perimeter, will be calculated for you.

Perimeter is the distance around. To find the perimeter of a right isosceles triangle, we add all the sides.

If any of the sides of the triangle is unknown, you first need to find each side. Using the Pythagorean Theorem, we know that the square of the hypotenuse (h) is equal to the sum of the other two sides. Since they are of equal length, we will use a to represent the other two sides.

Let's assume a is the known side, and it is equal to 5 cm.

Let us find the unknown sides:

Now that we know the length of each side, we may add them to arrive at the perimeter. So the perimeter (P) of this isosceles right triangle is:

To find the area of an isosceles right triangle, we use the formula:
area = ½ × base × height

In this instance, one of the equal sides is considered the base and the other the height. So, if the two equal sides have a measurement of 4cm, insert the measurements for the base and the height to find the actual area.

Next, follow these steps:

1. Substitute in the values: area = ½ × 4 × 4
2. Find the area area = 8 cm²

We will also employ the Pythagorean theorem to calculate the lengths of the two equal sides given the hypotenuse.

Substitute in the value of the hypotenuse - if the hypotenuse is equal to 5 cm, then:

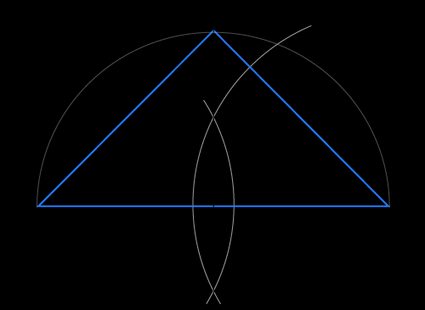
To construct a right isosceles triangle, you will need your book, a ruler, and a compass. Now that you have the tools you need, let's get started:

1. Use your ruler to draw a horizontal line on the page.
2. Mark a point on one end of the line.
3. We will call that point a.
4. Place your compass on the point marked a, and extending the drawing end a little beyond the center of the line, draw an arc that cuts through the line and extends upwards, creating a half-circle.
5. Draw a point on the other end of the line with your pencil.
6. Name this point b.
7. Place your compass on point b and, extending the drawing end a little beyond the center of the line, draw another large arc as you did before. These two arcs should intersect at the top and bottom.
8. Using your ruler and pencil, draw a line through the points where the arcs intersect.
9. Label the point where the two lines now bisect each other, o.
10. Place your compass at o and draw an arc that cuts line ab at both ends and the perpendicular line at one end.
11. Name the point where the arc passes through the perpendicular line c.
12. Use your ruler and pencil to draw a line from point a to c.
13. Repeat the above step from point b to point c.

Once you have completed these steps, you should now have an isosceles right triangle 😀.

Here is a list of related calculators:

• Isosceles triangle calculator;
• Isosceles triangle find A calculator;
• Isosceles triangle angles calculator;
• Isosceles triangle area calculator;
• Isosceles triangle side calculator;
• Isosceles triangle height calculator;
• Triangle vertices calculator.