Last updated: Jul 28, 2024

Tanh Calculator

Q: How do I compute the arc hyperbolic tangent?

To compute the value of arc hyperbolic tangent at x , follow these steps: Verify your x is a value between -1 and 1 . If it is not, you cannot compute tanh inv for this x ! Compute 1 + x and 1 - x . Perform the division (1 + x)/(1 - x) . Find the natural logarithm of the result. Divide by 2 . That's it!

Q: How do I get tanh in a calculator?

To compute tanh(x) with a basic calculator: Make sure your calculator can perform exponentiation. Compute exp(x) . Store the result at every step - use the memory of your calculator or just a piece of paper. Compute exp(-x) . Compute (exp(x) - exp(-x)) / (exp(x) + exp(-x)) . That's it! You can use an online tanh calculator to verify your result.

Q: What is the value of tanh 0?

The answer is 0 . You can read this value from the graph of tanh x as well as conclude it from the fact that tanh is an odd function, i.e., it satisfies tanh(-x) = -tanh(x) . Plugging in x = 0 , we get tanh(0) = -tanh(0) , which immediately gives tanh(0) = 0 , as claimed.

Q: Is tanh the same as arctan?

No , cosh stands for the hyperbolic cosine function , which is different from (yet related to, in some sense) the standard cosine function (cos) . The notation cos -1 is a bit ambiguous and may denote, depending on the context, the inverse cosine function ( arccos(x) ) or the multiplicative inverse ( 1/cos(x) ). Neither of them, however, is the same as cosh!

Created by Anna Szczepanek, PhD

Anna Szczepanek

PhD, Jagiellonian University in Kraków, Poland

Website

Holds a Ph.D. degree in mathematics obtained at Jagiellonian University. An active researcher in the field of quantum information and a lecturer with 8+ years of teaching experience. Passionate about everything connected with maths in particular and science in general. Fond of coding, she has a keen eye for detail and perfectionistic leanings. A bookworm, an avid language learner, and a sluggish hiker. She is hopelessly addicted to coffee & chocolate – the darker and bitterer, the better. See full profile

Check our editorial policy

Reviewed by Luis Hoyos

Luis Hoyos

Luis Hoyos is a fresh graduate Mechanical Engineer with thermodynamics and fluids mechanics expertise. He's interested in learning new things and applying them to real-life problems. Luis also likes to build tools that make repetitive and boring tasks a breeze, like calculators (surprise?). When he's not creating calculators, he's in the process of building the size of the tissue attached to his bones, aka bodybuilding. He also loves being with his little cat and seeing her do crazy things. See full profile

Check our editorial policy

New

Table of contents

What is tanh in math?Graph of hyperbolic tangent How do I compute the arc hyperbolic tangent?How to use this tanh calculator?Omni tools for hyperbolic functions FAQs

This tanh calculator is the ultimate tool you need to deal with the hyperbolic tangent function! In what follows, we will explain what tanh is in math and how to calculate both the inverse and the derivative of tanh. We won't forget to give you extra tips on how to use this hyperbolic tangent calculator most efficiently. Let's go!

What is tanh in math?

We define tanh (that is, the hyperbolic tangent function) as follows:

\small \tanh x = \frac{\mathrm{e}^x - \mathrm{e}^{-x}}{\mathrm{e}^x + \mathrm{e}^{-x}}

Okay, just some exponents and division, no big deal. It may not, however, be obvious at all why this function is called hyperbolic tangent. What does it have to do with tangents and hyperbolas?

Well, it's a slightly longer story. First, there exist functions called hyperbolic sine and hyperbolic cosine. Their definitions read:

\small \sinh x = \tfrac{1}{2}(\mathrm{e}^x - \mathrm{e}^{-x}) \\[0.5em] \cosh x = \tfrac{1}{2}(\mathrm{e}^x + \mathrm{e}^{-x})

They are called hyperbolic because the points ( $\cosh x$ , $\sinh x$ ) trace a (part of a) hyperbola in the standard Cartesian coordinate system.

And just as the normal tangent function is the ratio of sine to cosine, also the hyperbolic tangent is the ratio of hyperbolic sine to hyperbolic cosine:

\small \tanh x = \frac{\sinh x}{\cosh x}

Hyperbolic cotangent function

Also, just as the standard cotangent function is the multiplicative inverse of tangent, there is a function called hyperbolic cotangent defined, unsurprisingly, as follows:

\small \coth x = \frac{1}{\tanh x} = \frac{\mathrm{e}^x + \mathrm{e}^{-x}}{\mathrm{e}^x - \mathrm{e}^{-x}}

if $x \not = 0$ .

Graph of hyperbolic tangent

Let's take a look at the plot of tanh:

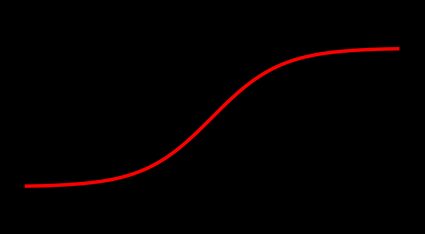
tanh graph — Geek3, CC BY-SA 3.0, via Wikimedia Commons

From the graph of the hyperbolic tangent function, we can deduce that:

tanh is an odd function, i.e., $\tanh(-x) = -\tanh(x)$ ;
tanh is increasing;
$\tanh(0) = 0$ ;
tanh is bounded: its values sit between $-1$ and $1$ ; and
tanh is a bijection, so it has an inverse.

The inverse function of tanh is called arc hyperbolic tangent. Let's discuss how to compute its values.

How do I compute the arc hyperbolic tangent?

To compute the value of arc hyperbolic tangent at x, follow these steps:

Verify your x is a value between -1 and 1. If it is not, you cannot compute tanh inv for this x!
Compute 1 + x and 1 - x.
Perform the division (1 + x)/(1 - x).
Find the natural logarithm of the result.
Divide by 2. That's it!

To summarize, the formula for the arc hyperbolic tangent function reads:

\operatorname{artanh} x = \tfrac 12\ln\frac{1+x}{1-x}

How to use this tanh calculator?

To use our hyperbolic tangent calculator, you only need to fill in the field x, and the value of tanh(x) will appear immediately. It couldn't be any easier, really.

If you want to find the inverse of tanh, that is, the arc hyperbolic tangent, you need to use the calc in reverse. That is, fill in the field tanh(x), and the value in x is exactly the value of artanh(x). Be careful! As we've explained above, the valid values of the inverse of tanh are the numbers between -1 and 1!

💡 Do you need other hyperbolic functions as well? Expand the section "Other hyperbolic functions" and they will appear :)

Omni tools for hyperbolic functions

Satisfied with the tanh calculator? Eager to learn more? Omni features a mini-collection of tools dedicated to hyperbolic functions:

FAQs

What is the derivative of tanh?

The derivative of the hyperbolic tangent is the square of the sech function. In fact, we have the following relationships: tanh'(x) = 1 - tanh²(x) = 1/cosh²(x) = sech²(x).

How do I get tanh in a calculator?

To compute tanh(x) with a basic calculator:

Make sure your calculator can perform exponentiation.
Compute exp(x). Store the result at every step - use the memory of your calculator or just a piece of paper.
Compute exp(-x).
Compute (exp(x) - exp(-x)) / (exp(x) + exp(-x)).
That's it! You can use an online tanh calculator to verify your result.

What is the value of tanh 0?

The answer is 0. You can read this value from the graph of tanh x as well as conclude it from the fact that tanh is an odd function, i.e., it satisfies tanh(-x) = -tanh(x). Plugging in x = 0, we get tanh(0) = -tanh(0), which immediately gives tanh(0) = 0, as claimed.

Is tanh the same as arctan?

No, cosh stands for the hyperbolic cosine function, which is different from (yet related to, in some sense) the standard cosine function (cos). The notation cos^-1 is a bit ambiguous and may denote, depending on the context, the inverse cosine function (arccos(x)) or the multiplicative inverse (1/cos(x)). Neither of them, however, is the same as cosh!

Related calculators

Interval Notation Calculator Partial Fraction Decomposition Calculator