Cosh Calculator

Omni's cosh calculator will help you quickly compute the values of the hyperbolic cosine function as well as discover its most important properties. In the short article below, we discuss the following topics:

• What cosh x is and why is it called hyperbolic?
• Can you meet cosh in real life? (Spoiler: yes)
• What does the plot of cosh look like?

We'll also touch upon more advanced topics, discussing the inverse cosh function as well as the derivative of cosh. Ready? Let's go!

Cosh is a function in math called hyperbolic sine. We compute its value as follows

As you most surely remember, the standard cosine function has a twin called sine. Hyperbolic cosine has a twin as well! The formula for hyperbolic sine is very similar to that of cosh:

Now, do you remember that by plotting the points ($\cos x$, $\sin x$) in the standard Cartesian coordinate system, we obtain a circle? Well, if you repeat this procedure with ($\cosh x$, $\sinh x$), you'll obtain... a hyperbola as in the picture below. That's why cosh and sinh are called hyperbolic functions!

(Well, more precisely, you'll obtain only the right-hand side part of the hyperbola, but that's enough to justify the name, isn't it?)

Okay, once we know what cosh is and how to compute it, let's plot its values and see what we can discover.

When we plot the values yielded by the formula defining cosh, we obtain the following graph:

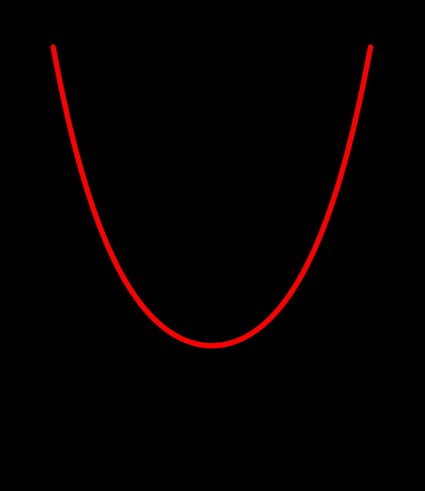
It looks a bit like a parabola, but when you plot the two in one picture, you'll clearly see a difference.

Looking at the plot of hyperbolic cosine, we can discover some of its properties :

• cosh is not periodic;
• cosh is an even function, i.e., $\cosh (-x) = \cosh (x)$;
• cosh is not bounded; and
• cosh is decreasing for x <0 and increasing for x<0; and
• $\cosh(0) = 1$.

As an even function, cosh is not a bijection, and so we cannot determine the inverse function right away. First, we need to restrict cosh to a part of its domain where it is bijective. For instance, to positive values. In the next section, we'll discuss how you can calculate the inverse of cosh.

The inverse cosh function is called arcosh, and its formula reads:

Surprised to see a logarithm? Well, you shouldn't be - recall that there are exponents in the definition of cosh!

The derivative of cosh is sinh, that is, the hyperbolic sine, defined as cosh(x) = (exp(x) - exp(-x))/2. Mind the signs! It's similar to what happens with standard sine and cosine functions, but there is no minus sign in front of sinh!

As you can see, this hyperbolic cosine calculator has two main fields: x and cosh(x). It's pretty straightforward to use it, but there are still some tips we want to share:

• If you want to calculate the value of cosh, simply enter the argument x, and the value of cosh(x) will appear.

• If you want to calculate the inverse function of cosh, enter the value into the cosh(x), and the result will appear in the field x. Remember that:

  • The valid arguments of the inverse of cosh are the numbers greater than or equal to 1; and
  • The result will be positive. The opposite number yields the same value of cosh, but the function must be restricted before it can be inverted.

• Finally, if you want to calculate the values of the derivative of cosh, you need to expand the 'Other hyperbolic functions' section. Several other hyperbolic functions will appear, among them sinh, which is exactly the derivative of cosh.

Happy with the hyperbolic cosine calculator? Hungry for more knowledge? Omni can serve some delicious bits of mathematics! Staying on the hyperbolic functions page of the menu, we offer the following delicacies:

• Hyperbolic functions calculator.
• Sinh calculator; and
• Tanh calculator.