String Girdling Earth Calculator

Imagine a string tightly wrapped around Earth's equator 🌍 Now, if you were to raise it 1 meter (3 ft 3 in) above the ground all around the equator, how much longer would the string need to be?

The string girdling Earth calculator is the perfect tool for solving this problem. It can quickly and easily help you determine the length of string needed to achieve a desired gap or the gap between the ground and the string after adding a given length to it.

Keep reading to learn:

• What's the string around the world problem;
• What's the gap that we get when we add 1 meter to the rope around the Earth;
• Does the diameter of Earth influence the result?; and
• How to use this string girdling Earth calculator.

The string girdling Earth, or the rope around the Earth problem, is a geometry puzzle that leads to a counterintuitive answer. At first glance, the question seems simple enough: if a string is tightly wrapped around the equator of a perfectly spherical Earth with a circumference of 40,000 km (25,000 mi) and then raised one meter off the ground at a uniform height along the equator, how much longer would the string need to be?

The circumference of Earth at the equator is approximately equivalent to running a 10k race 4,000 times, or flying from New York to London 6 times, or roughly 1/10th of the distance between Earth and the Moon — but despite all that, raising the string 1 meter off the ground only requires an additional 6.3 m (21 ft) or 2π m of string. This seems counterintuitive: 6.3 m is less than 1% of Earth's perimeter. So, how is this possible?

You'll see that the math behind this result is actually quite simple. All we need to know is the perimeter formula of a circumference:

Our problem involves two situations: initially, we have the tightly wrapped string around the world, and then we raise that string 1 meter off the ground.

The initial length of the string (represented as $L$) is equal to the Earth's perimeter in terms of its radius ($R$):

Once the rope is raised, we'll use the perimeter formula for the second scenario too — but this time with the new radius ($R+d$). This scenario is illustrated below:

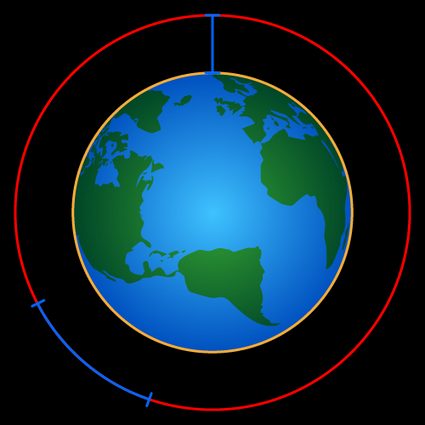
When we raise the rope to a distance $d$ above the ground, the perimeter is equal to the sum of the initial length of the string ($L$) and the additional length needed ($\Delta L$):

This leaves us with two expressions:

By substituting the top expression into the bottom one and rearranging, we're left with one simple equation:

This means that the extra string length depends only on the difference between the initial radius ($R$) and the final radius ($R-d$), which is $d$. Surprisingly, Earth's radius doesn't appear in the expression for $\Delta L$ at all! 🤯

Now that we know this, it makes sense that raising the rope by 1 meter (3 ft 3 in) results in a relatively small extra length of approximately 6.3 meters (21 ft) when compared to the circumference of Earth at the equator (40,000 km or 25,000 mi).

Another way to approach this problem is by splicing a given amount of string into the original length and determining if the resulting gap will be large enough for the passage of a particular object. For example, if we add 1 meter (3 ft 3 in) to the string, which is the tallest object that could fit through the gap: a car 🚗, a cat 🐱, a mouse 🐭, or a thin knife blade 🗡?

To solve this problem, we'll assume that the height of the car is 150 cm (5 ft), the height of the cat is 15 cm (6 in), the height of the mouse is 5 cm (2 in), and the height of the blade is 5 mm (0.2 in).

As you may have guessed, we can solve this with the equation we derived in the previous section:

Before we dive into the calculations, would you like to make a guess? Note that according to this equation, the resulting gap ($d$) should be smaller than the amount of string added ($\Delta L$). What might the answer be? Take a moment to make a guess before we continue with the calculation.

Have you made a guess? Let's continue.

To simplify the calculation, we can rearrange the equation to solve for $d$:

Now let's proceed to substitute the known value of $\Delta L = 1 \ \rm m$ (3 ft 3 in), we get:

The resulting gap between the string and the ground would be approximately 16 cm (6.3 in), enough room for the passage of a cat! Did you get it right? 🐱

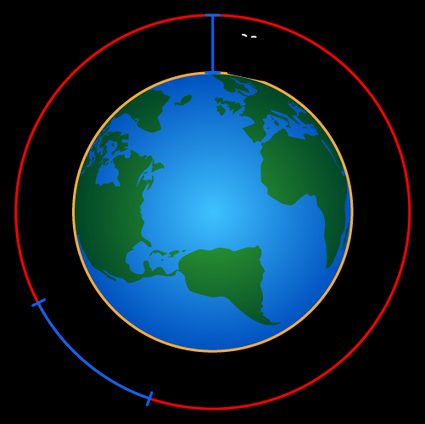
As we suspected earlier, this gap is smaller than the amount of string added!

Did you get the correct answer, or were you off by miles? Don't worry — we've got you covered with our string girdling Earth calculator! Here's how you can use it:

1. Head to the calculator's Test it yourself! section. Can't see it? Answer at least one of the initial problems relying solely on your intuition — only then the full potential of our tool will be revealed to you!

2. To determine the gap, enter the known length of string to be spliced into the calculator. The tool will then calculate the resulting gap or distance between the ground and the new position of the string.

3. Alternatively, if you want to find the length of string that needs to be spliced, input the known gap distance into the calculator. The tool will then calculate the required length of string that needs to be joined to achieve that gap distance.