Ratios of Directed Line Segments Calculator

The ratios of the directed line segments calculator will help you calculate the coordinates of the point that partition the line segment in a given proportion. This article will explore what a directed line segment is, how to partition a line segment with a given ratio with some examples, segment partition formula, and frequently asked questions.

If you're partitioning your line segment into two halves, our midpoint calculator will serve you equally well.

A line segment $AB$ is a part of a line bound by two endpoints $A$ and $B$ where $A \neq B$. A directed line segment $\overrightharpoon{AB}$ is a line segment with a definite direction – it is the line segment directed from $A$ to $B$.

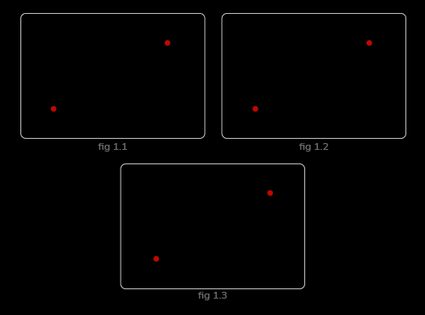
While the line segment $AB$ can also be written as $BA$, the same is not true for the directed line segment $\overrightharpoon{AB}$. This is because $\overrightharpoon{AB}$ is directed from $A$ to $B$, whereas $\overrightharpoon{BA}$ is directed from $B$ to $A$.

In the next section, we shall answer that burning question in your mind: how do you divide a segment into given ratios?

A point $P$ lying on the directed line segment $\overrightharpoon{AB}$ will divide into two line segments. There are two ways to divide a line segment:

1. Internally, when the point $P$ lies somewhere within the segment $\overrightharpoon{AB}$; and
2. Externally, when the point $P$ lies somewhere on the extended line segment $\overrightharpoon{AB}$.

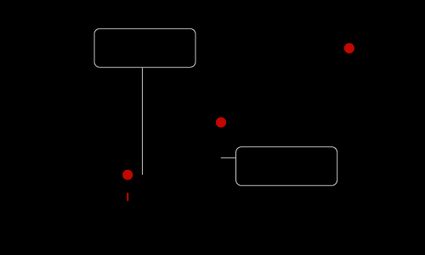
To partition the line segment $\overrightharpoon{AB}$ internally into the ratio $m:n$, the point $P(p_x,p_y)$ must lie on $\overrightharpoon{AB}$ such that it is $\frac{m}{m+n}$ away from $A$ and $\frac{n}{m+n}$ away from $B$.

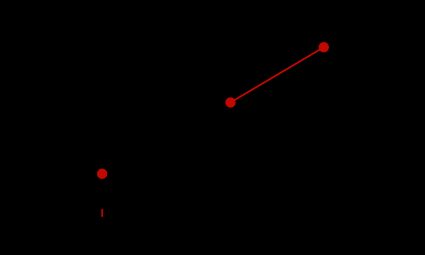
On the other hand, to partition the line segment $\overrightharpoon{AB}$ externally into the ratio $m:n$, the point $P(p_x,p_y)$ must lie on the extended line segment $\overrightharpoon{AB}$ such that it is $\frac{m}{m-n}$ away from $A$ and $\frac{n}{m-n}$ away from $B$.

Now that you know the concept of breaking a line segment into a ratio let's put together a formula for a directed line segment divided by any point $P$.

For the internal partition of $\overrightharpoon{AB}$:

And for the external partition of $\overrightharpoon{AB}$:

where:

• $P$ – Any point that partitions the directed line segment $\overrightharpoon{AB}$;
• $p_x,p_y$ – The x- and y-coordinates of the point $P$;
• $m,n$ – Ratio $m:n$ into which the point $P$ divides $\overrightharpoon{AB}$;
• $x_1,y_1$ – The x- and y-coordinates of the endpoint $A$ of $\overrightharpoon{AB}$; and
• $x_2,y_2$ – The x- and y-coordinates of the endpoint $B$ of $\overrightharpoon{AB}$.

Now that you know the ratio of line segments formula, let's discuss it further, along with some examples of segment partition calculation.

To find the point P(p_x, p_y) that internally divides the line segment AB into the ratio m:n, follow these steps:

1. Calculate p_x using p_x = (mx₂ + nx₁)/(m + n), where x₁ and x₂ are the x-coordinates of A and B respectively.
2. Determine p_y using p_y = (my₂ + ny₁)/(m + n), where y₁ and y₂ are the y-coordinates of A and B respectively.

To find the point P(p_x, p_y) that externally divides the line segment AB into the ratio m:n, follow these steps:

1. Compute p_x using p_x = (mx₂ - nx₁)/(m - n), where x₁ and x₂ are the x-coordinates of A and B respectively.
2. Find p_y using p_y = (my₂ - ny₁)/(m - n), where y₁ and y₂ are the y-coordinates of A and B respectively.

For example, consider a line segment $\overrightharpoon{AB}$ with the endpoints $A(1,2)$ and $B(4,6)$. The direction of this segment would be from $A$ to $B$. To find a point that divides this segment internally in the ratio $2:3$, we can use the internal partition formula as follows:

Note that to say that the point $P(2.2,3.6)$ divides $\overrightharpoon{AB}$ in the ratio $2:3$ is the same as saying that the point $P(2.2,3.6)$ lies ${\frac{2}{5}}^{th}$ away from the endpoint $A(1,2)$ and ${\frac{3}{5}}^{th}$ away from the endpoint $B(4,6)$.

Now, if we want to divide the same line segment externally in the same ratio, then we shall employ the formula for external partition of the line segment:

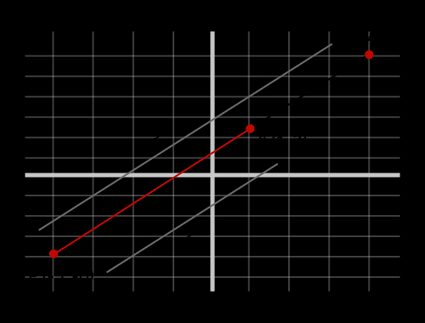
See how easy it is to partition a line segment in a given ratio?😉 Go ahead and try some practice problems and master this method! You can always verify your results using this calculator to divide line segments.

This ratios of directed line segments calculator is beneficial to find the point that divides a directed line segment in a given ratio or to find the ratio in which a given point splits the line segment.

1. Choose the type of partition between internal and external in the The line is partitioned... field. By default, we set it as an internal partition.

2. Enter the coordinates of the endpoints of the segment. Ensure that you're getting the direction of the line segment correct. In this calculator, the direction is always from $A(x_1,y_1)$ to $B(x_2,y_2)$.

3. This step depends on whether you want to find the point or the ratio:

   • If the ratio is the given value, enter the given ratio in the corresponding fields, and the coordinates of the point appear in their respective fields, along with a helpful graph. Otherwise, leave the ratio fields empty.
   • If the coordinates of the point are the given value, enter these coordinates in the corresponding fields, and the resulting ratio will appear at the bottom.

You now have a simple tool to help you calculate the partitioning of a line segment anytime you need it! Also check out our Golden ratio calculator or Endpoint calculator for more line segment partition calculations.

If you know the coordinates of the endpoints of the line segment, you can easily find its mid-point (x_m, y_m) using these steps:

1. Calculate the average of the x-coordinates of the end-points to get the x-coordinate of the mid-point. x_m = (x₁ + x₂)/2.
2. Determine the average of the y-coordinates of the end-points to obtain the y-coordinate of the mid-point. y_m = (y₁ + y₂)/2.
3. Verify these results using our Midpoint Calculator or Ratios of Directed Line Segments Calculator.

To divide a line segment AB into three equal parts, you need to find two points P(p_x, p_y) and Q(Q_x, Q_y) on AB, such that they each divide AB into the ratios 1:2 and 2:1:

1. Calculate the x-coordinate p_x of the point P using the formula p_x = (2x₂ + x₁)/3, where x₁ and x₂ are the x-coordinates of A and B respectively.

2. Compute the y-coordinate p_y of the point P using p_y = (2y₂ + y₁)/3, where y₁ and y₂ are the y-coordinates of A and B respectively.

3. Determine the x-coordinate q_x of the point Q using q_x = (x₂ + 2x₁)/3.

4. Find the y-coordinate q_y of the point Q using q_y = (y₂ + 2y₁)/3.

5. Put these coordinates together to get the points P(p_x, p_y) and Q(q_x, q_y).

A point P lying one-third of the way from the endpoint A on the line segment AB will divide it in the ratio 1:2. To find this point, follow these simple steps:

1. Calculate the x-coordinate p_x of this point using the formula p_x = (2x₂ + x₁)/3, where x₁ and x₂ are the x-coordinates of A and B respectively.

2. Compute the y-coordinate p_y of this point using p_y = (2y₂ + y₁)/3, where y₁ and y₂ are the y-coordinates of A and B respectively.

3. Put them together to obtain the desired point P(p_x, p_y).