Manhattan Distance Calculator

Are you wondering how far you have to walk to school? Maybe you're planning the route for your morning jog? Or are you just sick and tired of plain old Euclidean geometry?

Welcome to the Manhattan distance calculator. Here, you will learn what the Manhattan distance is, what it is used for, and how to calculate the Manhattan distance between two coordinates of your own.

The Manhattan distance is a distance metric between two points. It's the sum of the absolute differences between these points' coordinates. It's also known by other names:

• The taxicab distance;
• The city block distance; and
• The snake distance.

Picture this: you're in a city like New York or San Francisco, where the streets are neatly laid out in a grid. To get from point A to point B, you have to walk from intersection to intersection along the grid — you can't walk diagonally through the city's blocks. In mathematical terms, you're constrained to traveling along the city's coordinate axes, unlike a bird. The number of city blocks you'd have to walk is called the Manhattan distance, and you can probably already see where its other names — taxicab distance, city block distance, and snake distance — come from.

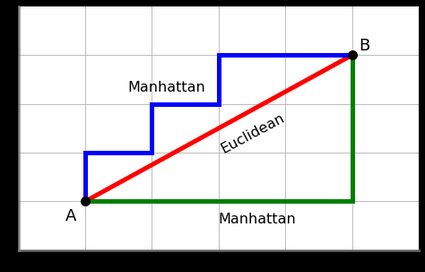
The Pythagorean theorem states that $c = \sqrt{a^2+b^2}$. While this is true, it gives you the Euclidean distance. If you were to rewrite the Pythagorean theorem for the Manhattan distance, it would instead be $c = a + b$.

Beyond determining how far away that coffee shop is in New York City, the Manhattan distance has a surprising number of applications. Here are just a few:

• In chess, the distance between squares for a rook is measured with the Manhattan distance, as this piece can only travel horizontally and vertically.

• In data science and machine learning, the Manhattan distance is used in speech recognition and image processing.

• In molecular biology, the Manhattan distance is used to decide where to splice genes and other molecules.

• In the popular Snake video game genre, the number of steps your snake has to move towards the next food item can be determined with the Manhattan distance; this is how it earned the nickname "snake distance".

With two N-dimensional points $\vec{a} = \left[ a_1, \dots, a_N \right]$ and $\vec{b} = \left[ b_1, \dots, b_N \right]$, the Manhattan distance $d$ can be calculated as:

Let's see how to calculate the Manhattan distance for a real-world example set in real-world Manhattan. Manhattan's east-west roads are called "streets", and its north-south roads are called "avenues". Let's say you live on the corner of 9th Street and 2nd Avenue, thus making your starting point $\vec{a} = [2, 9]$. You want to buy some milk at the grocery store on the corner of 5th Street and 3rd Avenue, so your destination is $\vec{b} = [3, 5]$. Using the Manhattan distance formula, the total distance you'd have to walk along the streets of New York is

city block lengths.

It might become clear now that it doesn't matter exactly how you walk from point A to point B. You can walk down to 5th Street first (covering the four blocks) and then go to 3rd Avenue (covering the last block), or you can go to 3rd Avenue before going to 5th Street. In the end, you're going to walk five city blocks — see why it's called the "city block distance"?

The Manhattan distance calculator is easy to use. It first asks you how many dimensions your points have, allowing points in up to four-dimensional space. You can then simply enter your points into the calculator, and it will output the Manhattan distance between your two points.