Last updated: Jun 21, 2024

Is it a Right Triangle Calculator

Q: Is it possible to draw a right isosceles triangle?

Yes, it is possible . To draw a right isosceles triangle, make sure the sides forming the right angle have equal lengths. Then connect their ends to draw a hypotenuse to form a right isosceles triangle. Drawing a diagonal inside a square will also let you draw right isosceles triangles.

New

Table of contents

What is a right triangle and how to tell if it is a right triangle?How to figure out if it is a right triangle - Calculator guide Other related calculators FAQs

This is it a right triangle calculator will help you determine whether or not a triangle qualifies to be a right triangle. This tool will be your companion when you just want to make sure you have a right triangle. In this right triangle calculator, you will learn:

What a right triangle is; and
How to figure out if a triangle is a right triangle using our calculator.

You're on the right track, so keep on reading.

What is a right triangle and how to tell if it is a right triangle?

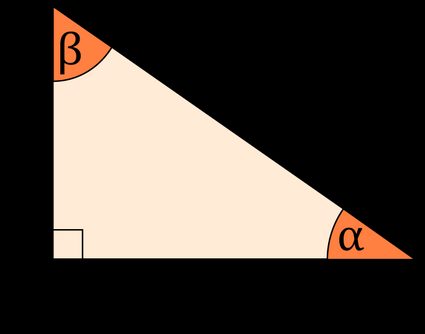
A right triangle is a triangle with one of its interior angles equal to 90°, hence the name. Since a triangle has a total of 180° for its interior angles, if one of its angles is 90°, that means its two remaining interior angles have a total of 90°, too. So to check if a triangle is right, its two remaining angles need to be complementary and acute (since every complementary angle is acute). In equation form, we express that as:

\begin{align*} \alpha + \beta + 90\degree &= 180\degree\\ \alpha + \beta &= 180\degree - 90\degree\\ \alpha + \beta &= 90\degree \end{align*}

where:

$\alpha$ and $\beta$ - Remaining angles of a right triangle that turn out to be complementary.

Aside from the relationship of the interior angles of a right triangle, its sides should also follow the Pythagorean theorem. That means that a right triangle has to have a hypotenuse, which we can denote as $c$ , which has a length equal to:

c = \sqrt{a^2 + b^2}

where:

$a$ and $b$ - Sides of the triangle forming a right angle.

Lastly, we can observe the following trigonometric functions when dealing with right triangles:

For angle $\alpha$ :

\begin{align*} &sin{(\alpha)} = \frac{a}{c}\\\\ &cos{(\alpha)} = \frac{b}{c}\\\\ &tan{(\alpha)} = \frac{a}{b} \end{align*}

For angle $\beta$ :

\begin{align*} &sin{(\beta)} = \frac{b}{c}\\\\ &cos{(\beta)} = \frac{a}{c}\\\\ &tan{(\beta)} = \frac{b}{a} \end{align*}

Note that:

$a$ - Length of side opposite angle $\alpha$ ;
$b$ - Length of side opposite angle $\beta$ ; and
$c$ - Length of the hypotenuse, or the side opposite the 90° angle.

If a triangle fails to meet even one of these conditions, then that triangle is not a right triangle.

How to figure out if it is a right triangle - Calculator guide

You can check your triangle in three different ways depending on the known parameters of the triangle you have. To use our right triangle calculator:

Choose in the Given selection your known set of parameters whether you know the 3 sides, angles α and β, or 2 sides and 1 angle.
Skip this step if you choose any of the first two options. If you chose 2 sides and 1 angle, select among the options which sides and angle you know.
Enter your known measurements depending on your selections.

After entering your last known parameter, our calculator will then display a message if your triangle is a right triangle or not.

FAQs

Is it possible to draw a right isosceles triangle?

Yes, it is possible. To draw a right isosceles triangle, make sure the sides forming the right angle have equal lengths. Then connect their ends to draw a hypotenuse to form a right isosceles triangle. Drawing a diagonal inside a square will also let you draw right isosceles triangles.

How do I tell if it is a right triangle?

To determine a right triangle, check if:

One of its interior angles is equal to 90°.
The sum of two of its angles is equal to 90°.
Its longest side, say c, is equal to the square root of the sum of the square of the two shorter sides, say a and b. In equation form: c = √(a² + b²).
It can meet any of these conditions:

sin(α) = a/c
cos(α) = b/c
tan(α) = a/b

where a is the side opposite angle α, b is the side adjacent to angle α, and c is the hypotenuse.