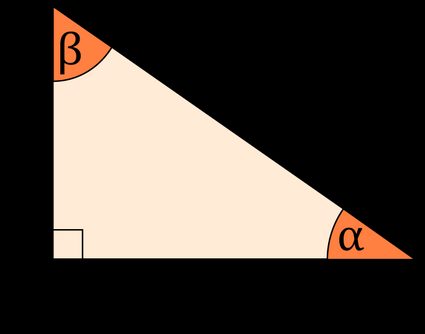
Right Triangle Side and Angle Calculator

Finding the missing side or angle couldn't be easier than with our great tool – right triangle side and angle calculator. Choose two given values, type them into the calculator, and the calculator will determine the remaining unknowns in a blink of an eye! If you are wondering how to find the missing side of a right triangle, keep scrolling, and you'll find the formulas behind our calculator.

There are a few methods of obtaining right triangle side lengths. Depending on what is given, you can use different relationships or laws to find the missing side:

1. Given two sides

If you know two other sides of the right triangle, it's the easiest option; all you need to do is apply the Pythagorean theorem:

a² + b² = c²

• If leg a is the missing side, then transform the equation to the form where a is on one side and take a square root:

  a = √(c² - b²)

• If leg b is unknown, then:

  b = √(c² - a²)

• For hypotenuse c missing, the formula is:

  c = √(a² + b²)

2. Given an angle and the hypotenuse

Apply the law of sines or trigonometry to find the right triangle side lengths:

• a = c × sin(α) or a = c × cos(β)

• b = c × sin(β) or b = c × cos(α)

3. Given an angle and one leg

Find the missing leg using trigonometric functions:

• a = b × tan(α)

• b = a × tan(β)

4. Given the area and one leg

As we remember from basic triangle area formula, we can calculate the area by multiplying the triangle height and base and dividing the result by two. A right triangle is a special case of a scalene triangle, in which one leg is the height when the second leg is the base, so the equation gets simplified to:

area = a × b / 2

For example, if we know only the right triangle area and the length of the leg a, we can derive the equation for the other sides:

• b = 2 × area / a
• c = √(a² + (2 × area / a)²)

If you know one angle apart from the right angle, the calculation of the third one is a piece of cake:

Given β: α = 90 - β

Given α: β = 90 - α

However, if only two sides of a triangle are given, finding the angles of a right triangle requires applying some basic trigonometric functions:

for α:

• sin(α) = a / c so α = arcsin(a / c) (inverse sine);
• cos(α) = b / c so α = arccos(b / c) (inverse cosine);
• tan(α) = a / b so α = arctan(a / b) (inverse tangent);
• cot(α) = b / a so α = arccot(b / a) (inverse cotangent);

and for β:

• sin(β) = b / c so β = arcsin(b / c) (inverse sine);
• cos(β) = a / c so β = arccos(a / c) (inverse cosine);
• tan(β) = b / a so β = arctan(b / a) (inverse tangent);
• cot(β) = a / b so β = arccot(a / b) (inverse cotangent).

To solve a triangle with one side, you also need one of the non-right angled angles. If not, it is impossible:

1. If you have the hypotenuse, multiply it by sin(θ) to get the length of the side opposite to the angle.

2. Alternatively, multiply the hypotenuse by cos(θ) to get the side adjacent to the angle.

3. If you have the non-hypotenuse side adjacent to the angle, divide it by cos(θ) to get the length of the hypotenuse.

4. Alternatively, multiply this length by tan(θ) to get the length of the side opposite to the angle.

5. If you have an angle and the side opposite to it, you can divide the side length by sin(θ) to get the hypotenuse.

6. Alternatively, divide the length by tan(θ) to get the length of the side adjacent to the angle.

Let's show how to find the sides of a right triangle with this tool:

1. Assume we want to find the missing side given area and one side. Select the proper option from the list. It's the third one.

2. Type in the given values. For example, the area of a right triangle is equal to 28 in² and b = 9 in.

3. Our right triangle side and angle calculator displays missing sides and angles! Now we know that:

   • a = 6.222 in
   • c = 10.941 in
   • α = 34.66°
   • β = 55.34°

Now, let's check how finding the angles of a right triangle works:

1. Refresh the calculator. Pick the option you need. Assume that we have two sides, and we want to find all angles. The default option is the right one.

2. Enter the side lengths. Our right triangle has a hypotenuse equal to 13 in and a leg a = 5 in.

3. Missing side and angles appear. In our example, b = 12 in, α = 22.62° and β = 67.38°.