Geometric Mean Calculator

Created by Hanna Pamuła, PhD

Reviewed by Bogna Szyk and Steven Wooding

Last updated: Apr 27, 2024

Table of contents:

With this geometric mean calculator, all calculations will be a pleasure! Just type the numbers of which you want to calculate the geometric mean, and the result will appear in no time. Remember that you may enter up to 30 numbers – extra boxes will appear as you go. If you're wondering what a geometric mean is and you're looking for a definition and formula of the geometric mean, then keep reading.

What is a geometric mean? Geometric mean definition and formula

A geometric mean – along with arithmetic, weighted, and harmonic means – is one of the most useful and common types of averages. Geometric mean may be defined as:

n-th root of the product of n values.

The $n$ -th root is at the same time the power of one divided by $n$ . Thus, we may state the geometric mean definition as:

The product of the values to the power of $1/n$ .

The general geometric mean formula looks then as follows:

$geometric mean formula$

Simply speaking, if you are wondering how to find the geometric mean, just multiply your values and take a square root (for two numbers), cube root (for three numbers), fourth root (for four numbers), etc.

Generally, the geometric mean applies only to positive numbers.

💡 You might also want to check out our harmonic mean calculator.

Geometric mean vs. arithmetic mean

In many cases, the arithmetic mean is the average we're looking for. However, there are some cases when the geometric mean is the preferable mean:

Different numeric ranges – e.g., we want to take into account two values assuming they are equally important: one from the $0$ - $5$ range and another from the $900$ - $1000$ range. Change of the smaller number, even a significant one (e.g., from $1$ to $5$ ), will result in a tiny difference in the arithmetic mean. The arithmetic mean neglects the smaller number, but that's the perfect case for the geometric mean.
The data is skewed downwards, and has large positive outliers – geometric mean can take care of that, in contrast to the arithmetic average.

Have a look at the table to find a direct comparison: geometric mean vs. arithmetic mean, with definitions, formulas, and applications of both types of averages:

	Arithmetic Mean	Geometric Mean
Definition	Sum of observations divided by the total number of observations	The $n$ -th root product of $n$ observations
General formula	$general formula of arithmetic mean$	$general formula of geometric mean$
Examples:
$4$ and $9$	$A = (4 + 9) / 2 = 6.5$	$A = \sqrt{4 \times 9} = \sqrt{36} = 6$
$4$ and $900$	$A = (4 + 900) / 2 = 452$	$A = \sqrt{(4 \times 900} = \sqrt{3600} = 60$
Applications	Many different fields, e.g., economics, biology, history, everyday life	Business (investment, growth, CAGR), math (rectangle area in terms of square side, analogically volume), image and signal processing (spectral flatness, filtering, choosing aspect ratio)
Relationship	Arithmetic mean ≥ Geometric mean (for non-negative data)

Also, the relationship between those two means may be defined as:

The logarithm of the geometric mean of the set of numbers is the arithmetic mean of the logs of these numbers.

For example, for three numbers:

\!\begin{split} \log&\left((a\times b\times c)^{\frac{1}{3}}\right)\\[1em] &=\frac{1}{3}\log\left(a\times b\times c\right)\\[1em] &=\frac{1}{3} \left(\log(a)\!+\!\log(b)\!+\!\log(c)\right) \end{split}

In other words, you can find the geometric mean by:

Calculate the logarithms of your data.
Find the arithmetic mean (often simply called average).
Taking the antilog of the result (remember that the antilogarithm is simply the exponentiation).

Geometric mean triangles and other applications in geometry

The geometric mean theorem (also called the right triangle altitude theorem) states that:

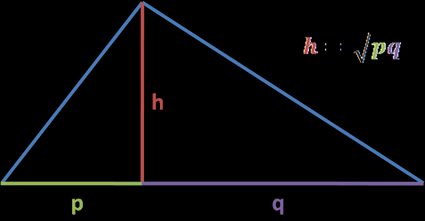
geometric mean formula applied to geometry. Right triangle, height from right angle divide hypotenuse h to p and q segments

Geometric mean of the two segments of a hypotenuse equals the altitude of a right triangle from its right angle.

h = \sqrt{p\times q}

Let's have a look at geometric mean triangles and proof of this theorem. We'll show that in two ways – using the similarity of the triangles and the Pythagorean theorem.

Following the image description, h is the altitude of a right triangle from its right angle, which splits the hypotenuse into two segments: $p$ and $q$ .

1. Triangles similarity

Triangle A with legs h and p and angle α, traingle b with legs h and q and angle β. Triangles similarity.

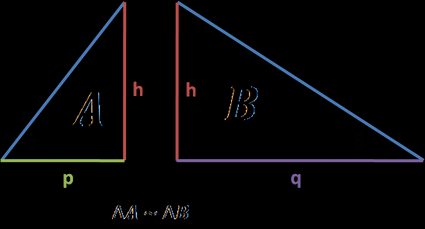
A hypotenuse is splitting the right triangle into two smaller triangles; let's call them triangles $A$ and $B$ . Triangle $A$ is similar to our base triangle (two angles in common, $90\degree$ and $\alpha$ ), and triangle $B$ is also similar to a base triangle (congruent $90\degree$ and $\beta$ ). From that, we can imply that triangle $A$ is similar to triangle $B$ .

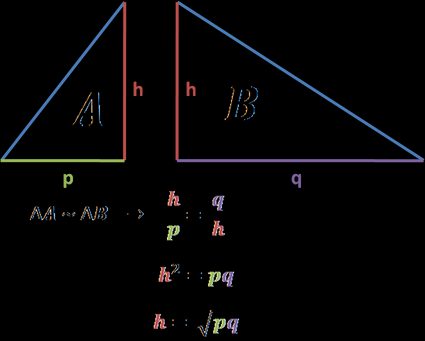
the image as above + formulas: h over p equals q/h, h times h equals p times q, h equals square root of p times q.

If the triangles are similar, we can write that the ratio between their congruent sides is the same. So for example longer leg of a triangle $A$ ( $h$ ) to shorter leg of that triangle ( $p$ ) equals triangle's $B$ longer leg to shorter leg ( $q / h$ ).
After simplifications, we're coming to the final formula:

\qquad h = \sqrt{p\times q}

If you're not sure how we did the ratios here to arrive at this result, check out our ratio calculator!

2. Pythagorean theorem

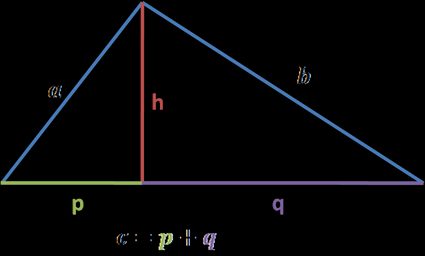
geometric mean formula and Pythagorean theorem. Right triangle, height from the right angle divide hypotenuse h to p and q segments. hypotenuse c equals p plus q.

Knowing the Pythagorean theorem, we can write equations for three right triangles:

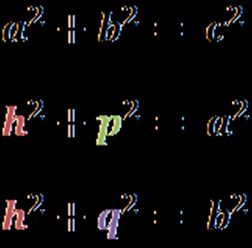
Pythagorean formulas for the three right triangles. a^2 + b^2 = c^2, h^2 + p^2 = a^2, h^2 + q^2 = b^2

Then, we can put altitude onto one side and add the last two equations:

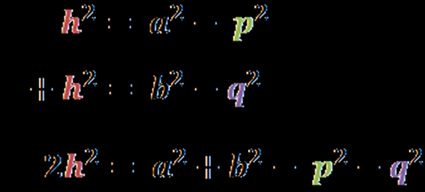
Formulas. h^2 = a^2 - p^2, h^2 = b^2 - q^2, 2h^2 = a^2 + b^2 - q^2 - p^2

After simplifications, we get to the final result:

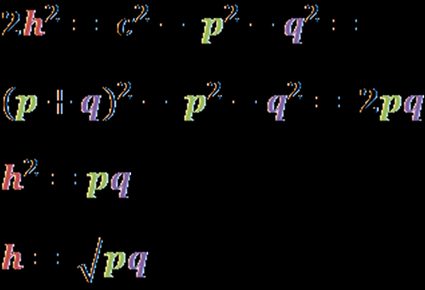
Formulas. Simplifications: 2h^2 = c2 - q^2 - p ^2 = (p+q)2 - q^2 - p^2 = 2pq, h^2 = pg, h = sqrt(pq)

It was a piece of cake, wasn't it?

The geometric mean is also applied to other geometric shapes and problems:

There are many geometric mean relationships in the ellipsis - e.g., taking the geometric mean of the maximum and minimum distances of the ellipse from a focus, you'll get the semi-minor axis.
Geometric mean of the distance to the closest and furthest point of a sphere is the distance to the horizon of a sphere.
Looking for the approximate derivation of a squaring circle problem, you'll also find the geometric mean formula essential.

How to find a geometric mean? An example on how to use geometric mean calculator

Let's take an easy example. Assume we want to know what is the geometric mean of $7$ and $12$ :

Type the first value into the box. It's $7$ in our case.
Enter the next value. For us, it's $12$ only. If you have more numbers than two, keep typing the values into separate boxes. Only eight are shown, but you can enter up to 30 numbers – they'll appear when the time comes.
Here you go! The geometric mean calculator displays the geometric mean on the go! Thanks to the tool, we found that the geometric mean of the two typed numbers is $9.1652$ . Great!

Hanna Pamuła, PhD

Values (you may enter up to 30 numbers)

Absolute changeAbsolute valueAdding and subtracting fractions… 72 more

Geometric Mean Calculator

What is a geometric mean? Geometric mean definition and formula

Geometric mean vs. arithmetic mean

Geometric mean triangles and other applications in geometry

How to find a geometric mean? An example on how to use geometric mean calculator

ASA triangle

Ellipse area

Humans vs vampires

Lost socks