Dividing Fractions Calculator

On the hunt for a tool that can divide any combination of fractions, mixed numbers, and whole numbers? If so, look no further - this dividing fractions calculator is the one for you! This calculator can help you with many different questions:

✔️ How to divide fractions with whole numbers?
✔️ How do you divide a whole number by a fraction?
✔️ How to divide mixed fractions?
❌ How to sum two fractions? And how to convert fractions to decimals and decimals to fractions?

Well, the last point isn't the purpose of this tool. Better check out our adding fractions calculator for tips and tricks on fraction addition, as well as two excellent converters, the fractions to decimals converter and the decimals to fractions calculator, designed to remove any doubts about fractions conversion. And for those searching for an all-in-one solution, we have something special – a comprehensive fraction calculator. Give it a go!

Dividing fractions is really similar to multiplying fractions. You just need to follow these steps to divide two fractions (for example, $\frac 4 5$ by $\frac 23$):

1. Calculate the reciprocal of your second fraction - the divisor (the fraction you want to divide by). To find the reciprocal, simply flip the number upside down so that the top number is now at the bottom and the bottom number is now above the line:

Remember that there's one number which doesn't have a reciprocal - $0$. So our second fraction can't have its top number equal to $0$ - and we hope that we don't need to remind you that you can't divide by zero, so the bottom number of a fraction can also never be zero.

2. Multiply your fractions. As a reminder, to multiply two fractions, you need to multiply the numerator by the other numerator and the denominator by the other denominator:

3. Finally, simplify the result, if needed:

And that's it!

That wasn't so difficult, was it? 😉 Our dividing fractions calculator shows you the step-by-step solution to your chosen example if you still have problems understanding how to divide fractions.

To summarize, you've just learned the general rules for dividing fractions. If you're searching for more specific instructions, like dividing mixed fractions or dividing fractions by whole numbers, keep reading!

When it comes to dividing fractions by whole numbers, it's pretty much the same as above: you need to multiply your fraction by a reciprocal – but this time, it's a reciprocal of the whole number. Let's look at an example, dividing $\frac 1 2$ by $3$:

1. Find the reciprocal of your whole number. As you may write every whole number as that number over $1$, then $3$ is $\frac 3 1$. Its reciprocal is then $\frac1 3$:

2. Multiply the fractions:

3. This time you don't need any fraction reduction, as the result will always be in its simplest form.

To sum up, the whole operation of dividing fractions by whole numbers looks as follows:

So, in other words, you can say that the denominator of your fraction is multiplied by the whole number.

Let's think about a word problem for the above example to help you intuitively understand dividing fractions by whole numbers.

The day after Halloween 🎃, two of your friends came for a visit. You'd like to offer them some food, but you only have half of a pumpkin pie in the house 😱. What proportion of the entire pie should each slice, if you want to divide it equally? Don't forget about yourself; you'd like to eat that yummy pie, too 🥧.

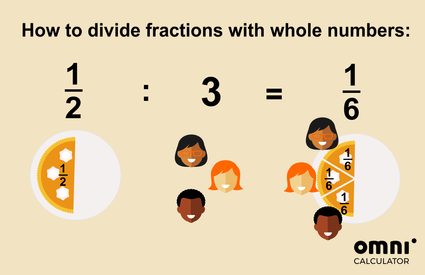
That's right! Every person will get one-sixth of a pie.

Dividing a whole number by a fraction should be a piece of cake for you (or a slice of pumpkin pie?🤔). The protocol is really similar, let's check how to divide $2$ by $\frac 1 6$:

1. Find the reciprocal of the divisor – the second fraction.

2. Do the fraction multiplication. As you can write $2$ as $\frac 2 1$:

And that's everything! In this case, you don't need to do any simplification.

Coming back to the pumpkin pie, you can imagine this problem as the question "How many slices that are one-sixth of a pie fit into two pies🥧🥧?"

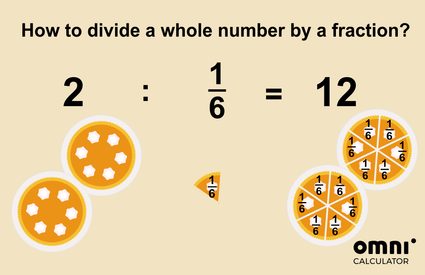
Yes, exactly! If you divide two pies into $\frac 1 6$ slice, you will get $12$ such slices in total.

We're pretty sure you've already guessed how to divide mixed fractions. You need only one additional step – to change the mixed fraction to an improper fraction:

Let's assume you want to divide $3\frac{1}{2}$ by $1\frac{4}{5}$:

1. Change any mixed numbers to improper fractions. Here is a quick reminder on how to do it: multiply the denominator by the whole number and add the numerator to get a new numerator. The denominator stays the same:

And:

Then, follow the standard procedure:

2. Find the reciprocal of the second fraction:

3. Multiply the fractions:

Of course, our dividing fractions calculator can deal with dividing mixed fractions 💪

As you've read the paragraph on how to divide fractions with whole numbers, we're sure this will be a walk in the park for you. Let's check how to calculate $\frac{3}{4}$ divided by $2$ as fractions, using this dividing fractions calculator:

1. Choose the fraction form. Let's pick the mixed number option, as you'd like to enter a whole number (however, simple fraction form is also fine, then you should write the whole number as the number over 1).

2. Input the first fraction. For the chosen example, put $3$ as a numerator (top number), and $4$ in the denominator box (it's the bottom number). You can ignore the whole number field or input $0$.

3. Enter the second value. Input $2$ to the whole number box and leave the other fields empty.

4. And that's it - the dividing fractions calculator worked out the answer! Now you know that $\frac{3}{4}$ divided by $2$ in fraction form is $\frac{3}{8}$.

If you need some details on what the calculations are for your example, check the step-by-step solution.

Finally, let's discuss a slightly more unusual case – dividing three fractions. To make it even more complicated, let's choose fractions in different forms: two fractions in their simple form (one negative) and one fraction that is a mixed number:

1. Select the proper form of the fraction. You need the mixed number option, as you have one mixed fraction.

2. Input the fractions:

   • 1^st fraction: $7$ as the whole number, $1$ as the numerator, $4$ as the denominator;

   • 2^nd fraction: empty or $0$ as the whole number, $5$ as the numerator, $6$ as the denominator; and

   • 3^rd fraction: empty or $0$ as the whole number, $-2$ as the numerator, $3$ as the denominator.

3. Check how to divide 3 fractions with a step-by-step solution. The result of the operation is $-\frac{261}{20} = -13\frac{1}{20}$.