Diamond Problem Calculator

Welcome to our diamond problem calculator, also known as a diamond problem solver. This intuitive tool allows you to enter any two numbers and the two others will appear. We've also prepared a compendium that answers all your burning questions about this topic.

Let's start by introducing what a diamond problem is and continue smoothly to some how to do diamond problems of various types tips. Are you ready?

Despite what you might think, the diamond problem doesn't have a lot in common with gemstones💎 or diamond rings💍 — though we can teach you how to calculate a diamond's weight. It is more closely related to what is often called a diamond in math ♦️ or cards🃏 - the rhombus, a quadrilateral shape. The diamond problem is a type of exercise that happens in a diamond shape 💠 - which we can also represent as a cross with 4 sections.

So, what is the diamond problem in math? It's where you fill in all four fields, related by some mathematical operation. The pattern of the numbers is constant:

• On the left and right side of the diamond, you have two numbers, sometimes called factors;
• In the top part you can find their product; and
• In the bottom section - their sum.

Solving the diamond problem means that you know only two numbers out of four, and you need to find the missing ones. And that's all!

There are three main types of diamond problems, and the diamond problem calculator can deal with all of them. If you're wondering how to do diamond problems in each of these cases, scroll down to the next sections.

This is the easiest case: you have two numbers, A and B, and you need to find the sum and product of them. For example, let's say that we want to solve the diamond problem for factors $13$ and $4$:

1. Calculate the product $= 13 \times 4 = 52$, and write the number on top.
2. Find the sum $= 13 + 4 = 17$, and input the value into the bottom part of the diamond.

You might meet this type of a diamond math problem in the first lesson about the diamonds - when your teacher first introduces the concept.

Let's have a look at a slightly more complicated case, where you have one of the basic numbers, and a product or a sum. The first thing to do is to calculate the factor missing from the diamond. Transform your equation is such a way to solve for the unknown value:

a) When you're given one factor and the sum, you can find a second factor by a simple subtraction:

And

So:

With both factors in hand, simply multiply them to get the last number: product $= 5 \times 6 = 30$.

b) If you know one factor and the product, divide the product by the factor to find the second product:

And:

So:

Then calculate the sum, use the following expression: sum $= \text{factor}\ A + \text{factor}\ B = 9 + 7 = 16$.

Remember, you can always quickly solve these diamonds or verify your answers with our diamond problem calculator.

Now we're coming to the last issue and the most common diamond problem: the case where you know the sum and the product of the two numbers, but you don't actually know the numbers themselves.

This type of diamond math problem is helpful when you're learning about factoring a quadratic equation. Why?

Let's say that we have a quadratic equation:

We would like to factor this equation, meaning that we'd like to present it in a form:

How to find these numbers - the roots of the quadratic equation? You know that their product must be equal to $12$, and that their sum is equal to $7$. And that's exactly what you're trying to find out in the diamond problem! 🙂 You can rewrite this question in the form of a diamond:

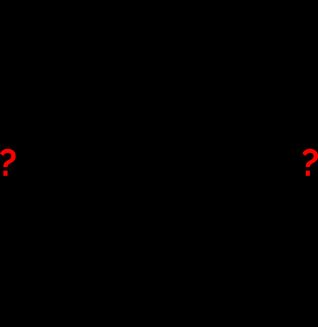
How to solve such a problem?

1. Start with the top number - the product of two numbers. Write down all possible pairs of numbers that give this as their product. You can, for example, calculate the prime factorization if it's a more complicated case. In our example, the product is equal to 12 - which two integer numbers could be multiplied together? The order of the factors doesn't matter, as multiplication (and addition) are commutative:

Don't forget the negative numbers:

2. Sum these two numbers, and check which combination gives the desired sum of 7:

And here it is! We can stop here, as we've found the two numbers which meet the condition 🎉

Sometimes it's very easy to guess the solution, as there are not many options. We're sure that you'll solve this a diamond problem in no time!

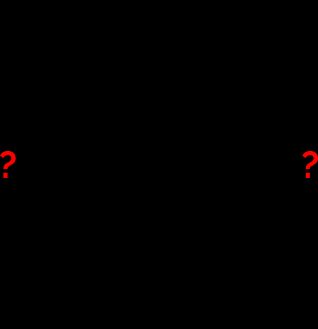
If not, enter the numbers into our diamond problem solver. That wasn't so difficult, was it? 🤦

It's really easy, believe us!

All you need to do is to input any two numbers and the diamond problem solver will find out the other two. What's more, the tool displays the solution in a diamond form. What more could you wish for? 😎

Please notice that in some specific cases you'll need to hit the refresh button ⟳ to use the calculator again 👍

The top number is -32, and the bottom is 4. To find the top, we multiply the side numbers. We add them together to find the bottom.

We use the diamond problem in addition, subtraction, multiplication, and division in maths. It is used to calculate integers, decimals, and fractions and for factoring trinomials.

Assuming that you are given two fractions on the left and right sides, say ¹/₂ and ⁵/₆, follow these steps to solve the problem:

1. Find the product of the fractions:
   ¹/₂ × ⁵/₆ = ⁵/₁₂

2. Place this answer (⁵/₁₂) at the top:

3. Find the sum of the fractions:
   ¹/₂ + ⁵/₆ = ⁶/₁₂ + ¹⁰/₁₂ = ¹⁶/₁₂

4. Place this answer (¹⁶/₁₂) at the bottom.

Voila! You solved the diamond problem.

Assuming the top number is 35, and the bottom is 12. Follow these steps to find the numbers to the right and left:

1. Find the factors of the top number:
   35, 1
   7, 5
2. Identify the factors which, when added together, equal to the bottom number:
   7, 5
3. Place these numbers on either side.

That's it. You have solved the diamond problem for the right and left numbers.