Cube Root Calculator
Our cube root calculator is a handy tool that will help you determine the cube root, also called the 3rd root, of any positive number. You can immediately use our calculator; just type the number you want to find the cube root of and it's done! Moreover, you can do the calculations the other way around and use them to cube numbers. To do this just type the number you want to raise to third power in the last field! It may be extremely useful while searching for so-called perfect cubes. You can read more about them in the following article.
Thanks to our cube root calculator, you may also calculate the roots of other degrees. To do so, you need to change the number in the degree of the root field. If you would like to learn more about the cube root definition, familiarize yourself with the properties of the cube root function, and find a list of the perfect cubes, we strongly recommend you keep on reading this text. In there, you can also find some tricks on how to find the cube root on a calculator or how to calculate it in your head.
If you are interested in the history of root symbols head to the square root calculator, where we discuss it.
Cube root definition
Let's assume you want to find the cube root of a number, x. The cube root, y, is such a number that, if raised to the third power, will give x as a result. If you formulate this mathematically,
∛x = y ⟺ y^3 = x
where ⟺ is a mathematical symbol that means if and only if.
It is also possible to write the cube root in a different way, which is sometimes much more convenient. It is because a cube root is a special case of an exponent. It can be written down as
∛(x) = x^(1/3)
A geometric example may help you understand this. The best example we can give would be that of the cube. Well, the cube root of a cube's volume is its edge length. So, for example, if a cube has a volume of 27 cm³, then the length of its edges is equal to the cube root of 27 cm³, which is 3 cm. Easy?
You should remember that in most cases, the cube root will not be a rational number. These numbers can be expressed as a quotient of two natural numbers, i.e., a fraction. Fractions can cause some difficulties, especially when it comes to adding them. If you are having trouble working with fractions, try our adding fractions calculator, which will help you immensely.
What is the cube root of...?
It is really easy to find the cube root of any positive number with our cube root calculator! Simply type in any number to find its cube root. For example, the cube root of 216 is 6. For the list of perfect cubes, head to the next section.
Note that it is possible to find a cube root of a negative number as well. After all, a negative number raised to the third power is still negative - for instance, (-6)³ = -216.
You need to remember, though, that any non-zero number has three cube roots: at least one real one and two imaginary ones. This cube root calculator deals with real numbers only, but if you're interested, we encourage you to read more on the topic of imaginary numbers!
Most common values - perfect cubes list
You can find the most common cube root values below. Those numbers are also very often called perfect cubes because their cube roots are integers. Here is the list of the ten first perfect cubes:
- cube root of 1:
∛1 = 1, since1 * 1 * 1 = 1; - cube root of 8:
∛8 = 2, since2 * 2 * 2 = 8; - cube root of 27:
∛27 = 3, since3 * 3 * 3 = 27; - cube root of 64:
∛64 = 4, since4 * 4 * 4 = 64; - cube root of 125:
∛125 = 5, since5 * 5 * 5 = 125; - cube root of 216:
∛216 = 6, since6 * 6 * 6 = 216; - cube root of 343:
∛343 = 7, since7 * 7 * 7 = 343; - cube root of 512:
∛512 = 8, since8 * 8 * 8 = 512; - cube root of 729:
∛729 = 9, since9 * 9 * 9 = 729; - cube root of 1000:
∛1000 = 10, since10 * 10 * 10 = 1000;
As you can see, numbers become very large quickly, but sometimes you'll have to deal with even bigger numbers, such as factorials. In this case, we recommend using scientific notation, which is a much more convenient way of writing down really big or really small numbers.
On the other hand, most other numbers are not perfect cubes, but some of them are still used often. Here is the list of some of the non-perfect cubes, rounded to the hundredths:
- cube root of 2:
∛2 ≈ 1.26; - cube root of 3:
∛3 ≈ 1.44; - cube root of 4:
∛4 ≈ 1.59; - cube root of 5:
∛5 ≈ 1.71; - cube root of 10:
∛10 ≈ 2.15;
Don't hesitate to use our cube root calculator if the number you want and need is not on this list!
Cube root function and graph
You can graph the function y = ∛(x). Unlike e.g. the logarithmic function, the cube root function is an odd function - it means that it is symmetric with respect to the origin and fulfills the condition - f(x) = f(-x). This function also passes through zero.
Thanks to this function, you can draw a cube root graph, which is shown below. We also encourage you to check out the quadratic formula calculator to look at other function formulas!
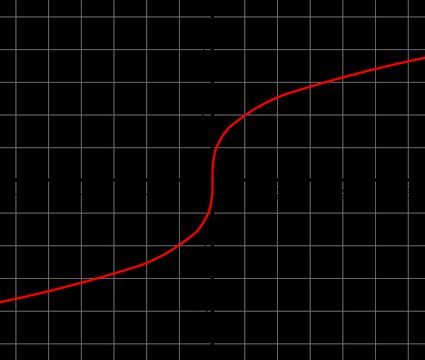
How to calculate cube root in your head?
Do you think that it is possible to solve simple problems with cube roots without an online calculator, or even a pencil or paper? If you think that it is impossible, or that you are incapable of doing it check out this method, it is very easy. However, it only works for perfect cubes. Forget all the rules in the arithmetic books and consider for a moment the following method described by Robert Kelly.
First of all, it is essential to memorize the cubes of the numbers from 1 to 10 and the last digit of their cubes. It is presented in the table below.
Number | Cube | Last digit |
|---|---|---|
1 | 1 | 1 |
2 | 8 | 8 |
3 | 27 | 7 |
4 | 64 | 4 |
5 | 125 | 5 |
6 | 216 | 6 |
7 | 343 | 3 |
8 | 512 | 2 |
9 | 729 | 9 |
10 | 1000 | 0 |
When you have a number you want to find the cube root of look first at the thousands (skip the last three digits). For example, for the number 185,193, The thousands are 185. The cube of 5 is 125 and of 6 is 216. Therefore it is obvious that the number you are searching for is between 50 and 60. The next step is to ignore all the other figures except the last digit. We can see that it's 3, so check your memory or in our table. You will find that the number you are searching for is 7. So the answer is 57! Easy?
Let's take another example and do it step by step!
- Think of the number that you want to know as a cube root. Let's take 17576.
- Skip the three last digits.
- Find the two closest cube roots that you know. The cube root of 8 is 2, and the cube root of 27 is 3. So your number is between 20 and 30.
- Look at the last digit. The last digit of 17576 is 6.
- Check your memory (or on our table) - the last digit 6 corresponds with the number 6. This is the last digit of your number.
- Combine the two: 26. This is the cube root of 17576!
We remind you that this algorithm works only for perfect cubes! And the probability that a random number is a perfect cube is, alas, really low. You've got only a 0.0091 percent chance of finding one between 1,000 and 1,000,000. If you're not sure about your number, just forget about that rule and use our cube root calculator :-)
How do I find the cube root on a regular calculator?
- First, you need to type the number for which you need to find the cube root
- Press
√(root key) two times - Press
x(multiplication sign) - Press
√(root key) four times - Press
x(multiplication sign) - Press
√(root key) eight times - Press
x(multiplication sign) - One last time, press the
√(root key) two times - And now you can press
=(equal to sign)! Here is your answer!
Don't you believe it? Check it one more time with another example!
Examples of cube root questions
Let's say you need to make a ball with a volume of 33.5 ml. To prepare it you need to know its radius. As you probably know, the equation for calculating the volume of a sphere is as follows:
V = (4/3) * π * r³
So the equation for the radius looks like this:
r = ∛(3V/4π)
You know that the volume is 33.5 ml. At first, you need to switch to different volume units. The simplest conversion is into cm³: 33.5 ml = 33.5 cm³. Now you can solve the radius:
r = ∛(100.5/12.56)
r = ∛(8)
r = 2
For a ball to have a volume of 33.5 ml, its radius should be 2 centimeters.
nth root calculator
With our root calculator, you can also calculate other roots. Just write the number in the Degree of the root field, and you will receive any chosen nth root calculator. Our calculator will automatically do all necessary calculations, and you can freely use it in your calculations!
So, let's take some examples. Let's assume you need to calculate the fourth root of 1296. First, you need to write the appropriate number you want to root - 1296. Then change the degree of the root to 4. And you've got the result! The fourth root of 1296 is 6.
Our nth root calculator also enables you to calculate the root of irrational numbers. Let's try it by calculating π-th root. Symbol π represents the ratio of a circle's circumference to its diameter. Its value is constant for every circle and is approximately 3.14, but you can use our ratio calculator to find its more precise value!
Let's say you want to calculate the π-th root of 450. First, write 450 in the number box. Then change the degree of the root - let's round and write 3.14 instead of π. And now you can see the result. It's almost 7.
Three solutions of the cube root
At the end of this article, we've prepared an advanced mathematics section for the most persistent of you. You probably know that positive numbers always have two square roots: one negative and one positive. For example, √4 = -2 and √4 = 2. But did you know that a similar rule applies to the cube roots? All real numbers (except zero) have exactly three cube roots: one real number and a pair of complex ones. Complex numbers were introduced by mathematicians a long time ago to explain problems that real numbers cannot do. We usually express them in the following form:
x = a + b*i
where x is the complex number with the real a and imaginary b parts (for real numbers b = 0). The mysterious imaginary number i is defined as the square root of -1:
i = √(-1)
Alright, but how does this knowledge influence the number of cube root solutions? As an example, consider the cube roots of 8, which are 2, -1 + i√3, and -1 - i√3. If you don't believe us, let's check it by raising them to the power of 3, remembering that i² = -1 and using the short multiplication formula (a + b)³ = a³ + 3a²b + 3ab² + b³:
2³ = 8- the obvious one,(-1 + i√3)³ = -1 + 3i√3 + 9 - 3i√3 = 8,(-1 - i√3)³ = -1 - 3i√3 + 9 + 3i√3 = 8.
Do you see it now? All of them equal 8!
FAQs
How do I find the cube root of a product?
The cube root of a product of two numbers is the product of the cube roots of these numbers. That is, the formula is ∛(a × b) = ∛a × ∛b.
What is the cube root of -8/27?
The answer is -2/3. To get this result, take these steps:
- Recall the formula
∛(a / b) = ∛a / ∛b. - Compute the cube root of
-8. Clearly,∛(-8) = -2. - Compute the cube root of
27: we have∛27 = 3. - The final result is
-2/3. Well done!
How do I write the cube root on a computer?
The Alt code for the cube root ∛ symbol is 8731. That is, to produce ∛, take these steps:
- Make sure the Num Lock is on.
- Press down one of the Alt keys.
- Holding down the Alt key, type the code
8731using the numeric keypad. - Let go of the Alt key. The cube root symbol will appear.
- Alternative method: copy the ∛ symbol (Ctrl+C) and paste it wherever you need it (Ctrl+V).