Complex Conjugate Calculator

Welcome to the complex conjugate calculator, where we'll learn all about the conjugate of a complex number. We'll start slow with an introduction to complex numbers and the conjugate definition. Then, we'll see some conjugation examples and see how conjugate pairs behave, i.e., what happens when we multiply by the conjugate.

If you've been asking yourself, "What is conjugation?" or "What is a complex conjugate?", you've come to the right place!

Life is full of surprises. And since mathematics is our whole life, it's bursting with surprises as well.

At the very beginning of your mathematical education, you were told how to add and subtract numbers. But there's a catch: you can't subtract, say, $5$ from $2$. A couple of years later, they tell you that, actually, you can, and the result is a negative number. Alright, fair enough. After all, what is a debt if not a negative number?

But there's more! When you get to multiplication and division, they teach you that, for instance, $7$ is not divisible by $4$. But later on, you get to fractions and find that, in fact, you can divide them to get $1\small{\tfrac{3}{4}}$(or $1.75$ if you prefer decimals). Again, it kind of makes sense since a chocolate bar costs $0.80$ and not a whole dollar.

Lastly, in higher grades, you get to learn about exponents and the inverse operation: root (you can learn more about roots in our root calculator). While not every number is a perfect square, you can still find, say, the square root of $3$, even though it's some crazy number whose decimal expansion goes on forever. And once you get to see the Pythagorean theorem (how do you calculate Pythagorean theorem?) and right triangles in general, you come to understand radicals more and more.

Wherever they appear, one thing is certain: the square root of a negative number doesn't exist…

Or does it?

Complex numbers are of the form $z = a + b\mathrm{i}$, where $a$ and $b$ are real numbers (i.e., any of the numbers that we learned about in school), and $\mathrm{i}$ denotes the square root of $-1$ ($\mathrm{i} = \sqrt{-1}$). The $a$ is often called the real part of $z$, while $b$ is called the imaginary part (yup, that's exactly what those big-headed mathematicians called it).

It may seem at first glance that complex numbers are too artificial to be of any use in real life. After all, they can't really appear in areas such as geometry…

Or can they?

In fact, they can. First of all, observe that for $z = a + b\mathrm{i}$, whenever we have $b = 0$, $z$ is simply a real number. Therefore, complex numbers are just an extension of what we've known so far and can broaden our perspective. They are extremely (and we mean EXTREMELY) important in modern physics and mathematics to describe certain processes more accurately. Let us mention a few to give you a taste:

• Quadratic and higher power polynomials;
• Wavelength; and
• Diffraction.

Now that we know what complex numbers are, we're ready to introduce conjugation. So what is a complex conjugate? Well, it's an operation that we'll study in the next section!

Let's start with the conjugate definition because it's so simple.

The conjugate of a complex number$z = a + b\mathrm{i}$ is the number $a - b\mathrm{i}$. We denote this operation by putting a horizontal line over the value like this:

It may seem like the conjugate in math is a simple, useless operation that doesn't change much. In fact, the conjugate of a number has a deeper meaning that we'll try to explain in a second.

Do you know how we mark real numbers on a line? With complex numbers, it's not that easy because we don't know if $\mathrm{i}$ is smaller or larger than $0$ (in fact, it's neither). Therefore, we need two axes to describe them, which together form the complex plane.

Above, we see an example of a complex number represented on the complex plane – in this case, it's $z = 2 + \mathrm{i}$. Just as it is on the image, the horizontal axis marks the real part (the one without $\mathrm{i}$, so it's $2$), and the vertical axis is the imaginary part (the one with $\mathrm{i}$, i.e., $1$).

So what is conjugation? It is the symmetric reflection of the point with respect to the real axis. To put it in simpler terms, imagine that you have a mirror along the horizontal line. Where would the reflection of $z$ be? Check the picture below:

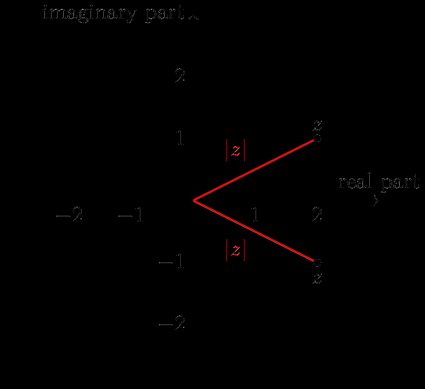
Note that:

1. Straight from the conjugate definition, if we apply conjugation twice, we'll get the number we started with (because we flip it to the other side and back again).

2. Conjugate pairs (the two numbers that are conjugates of one another) are on opposite sides of the real axis.

3. The only numbers that are conjugate-invariant (i.e., conjugation doesn't change them) are those whose imaginary part is equal to zero, which means that they are just real numbers. They lie on the horizontal axis, and therefore flipping them does nothing.

4. The distance from $0$ to the complex number $\rm i$ is the same as from $0$ to its conjugate. We denote this value as $|z|$ and call it the absolute value of $z$, or the modulus of $z$ (read more on our absolute value calculator). We calculate it in the same way we find the length of a vector in regular 2-dimensional space:

So, what is a complex conjugate? It is the same number but with the inverse sign in the imaginary part. Or, if you prefer to look at it geometrically, the conjugate in math means flipping the point on the complex plane to the other side with respect to the real axis.

"But what is conjugation good for?" Well, now that we know the definition, we're ready to see some conjugation examples and useful properties – especially what happens when we multiply by the conjugate.

Shall we?

Why don't we first give you a nice table with several conjugation examples and then study it in detail? No objections? Well, we hear none, so here it is!

Now, let's take a closer look at those conjugate pairs. In essence, we have described all that happens there in the above section, but it's always refreshing to look at numbers instead of letters and symbols, don't you think?

• The two first rows are the most standard conjugation examples: the sign next to the imaginary part changes from $+$ to $-$ or vice versa.

• From the second and third rows, we see that the conjugate of the conjugate of a complex number is the same as the number itself. In simpler words, if you conjugate in math twice, you'll go back to the very beginning.

• Lines 4 and 5 show that conjugation applied to a real number doesn't change it, no matter its sign.

• The last two rows tell us that if a complex number has no real part, then it simply changes its sign. In fact, the real part, which is $0$ here, stays as $0$.

The last thing we'd like to mention in this section is a very interesting property of the conjugate in math, i.e., what happens when you multiply by the conjugate.

Firstly, let's look at the matter symbolically. Let $z=a + b\mathrm{i}$ be a complex number. What is the complex conjugate of such a number? Yup, nothing changed here - it's $a - b\mathrm{i}$. Now, let's try to multiply them.

Where the fourth line comes from the fact that $\rm i$ is the square root of $-1$, so $\mathrm{i}^2$ is $-1$.

So what do we get if we multiply $z$ by the conjugate? We get the square of the absolute value. Simple as that, no strings attached. It's what happens every time.

The only thing we have left to discuss is how to use the complex conjugate calculator. We've already learned that the conjugate in math is a piece of cake, but why don't we go through it quickly? Oh, come on, for old-time's sake?

Suppose that you've just learned that there is such a thing as complex conjugation, and your teacher gives you ten complex numbers and tells you to find their conjugates. They then sit at their desk, hoping that it will keep the class busy long enough to take a quick nap.

The numbers are:

Fair enough, there are quite a few of them. But it's not something that the complex conjugate calculator or we can't deal with!

Let's begin with (surprise, surprise) the first one: $2 + 2\mathrm{i}$. When we look at the complex conjugate calculator, we see the formula at the top, which also gives the notation used below. Here, we see that $a$ is the real part, and $b$ is the imaginary part of our complex number. This means that we have to put:

Once we feed the complex conjugate calculator with both, the answer will pop up: the conjugate is $2 - 2\mathrm{i}$, so we can write this first result in our table.

Next, we have $5 - \mathrm{i}$. Observe that here, at first glance, we have nothing next to $\mathrm{i}$. However, it's similar to how we view polynomials: if we have $x^2 - x + 7$, it doesn't mean that we have nothing next to $x^2$ and $x$. We have $1$ and $-1$, respectively. It's just a convention that we don't write the ones.

In the end, we have to input the following:

which gives $5 + \mathrm{i}$.

Next, we have $-7$. Here indeed, we have no imaginary part. In other words, it vanishes, so it's equal to $0$. This translates to

And returns $-7$.

All in all, the filled table should look as follows:

Finished! Wouldn't it be great if these questions came up on the test?

Knowing your teacher, they'll probably tell you to add one more column and calculate the absolute value of the numbers once you are done. Oh, how lucky we are that the complex conjugate calculator does that, too! Just check the last field in the Result section.

With Omni, we can solve every math problem in no time!