Bit Shift Calculator

The bit shift calculator lets you execute bit shifts to the left and bit shifts to the right. The logical shift operation can be done with input from the binary, octal, and decimal number systems, and the calculator gives the results in signed and unsigned representations.

A bit shift is a bitwise operation executed on a binary number. To understand this better, let's take a look at the concept step by step.

Binary numbers are numbers founded on the base 2 system. You can refresh your knowledge of this other numerical system at the binary converter. Base 2 means that each digit can only have the values $0$ and $1$, representing a bit, the smallest unit of digital information. One bit can only display two logical states: on or off. To make up larger amounts of information, bits are lined up to form binary numbers. With those, arithmetic operations like binary subtraction can be executed trouble free.

Binary numbers can be converted to numbers in the decimal system. In the case of negative numbers in the decimal system, there is a so-called signed representation, allowing to display those in the binary system.

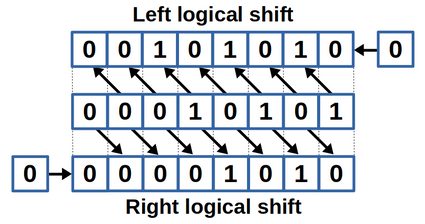
So what is a bit shift? A bit shift is an operation where a succession of bits is moved either to the left or the right. For logical bit shifts, the bits shifted out of the binary number's scope are lost, and 0's are shifted in on the other end. This differentiates this method from the circular and arithmetic bit shift. Bit shifts are not the only bitwise operations; further important ones are AND, OR, and XOR: meet them at Omni's logic gate calculator and bitwise calculator!

The picture above shows an example of bit shifts to the right and left. Input is the binary number $0001\ 0101$, or $1\cdot2^4 + 1\cdot2^2 + 1\cdot2^0$.

• The right bit shift moves every bit of the input one position to the right. Thereby, the least significant bit is lost, while a $0$ is pushed in on the other end.
• The left bit shift moves every bit of the input one position to the left. A $0$ is pushed in on the right end to fill up the bit succession.

The bit shift is an important operation to perform mathematical operations efficiently. In the example above, we shifted the binary number $0001\ 0101$, or $21$ in the decimal system, one bit to the left. The result is $0010\ 1010$, or $42$ in the decimal system. So shifting one bit to the left is equal to multiplying a number by the factor $2$. Shifting two bits means multiplying by $4$, $3$ bits by $8$, and so on. This concept also works the other way around: a bit shift to the right equals a division by $2$. Additionally, bit shifts are also significant for the digital electronics field of registers.

You now know what a bit shift is and how to execute a logical shift. So let's take a look at how to use the bit shift calculator. As an example, we will execute a bit shift left. We shift the number $27$ in the decimal system $2$ bits to the left, using the tool as a left shift calculator.

1. Choose the number of bits in the binary representation. Since 8 bits enable the input of numbers in the range $-128$ to $127$ in the decimal system, this is sufficient for our cause.
2. Choose your input datatype. The bit shift calculator supports numbers from the binary, octal, and decimal systems. We choose decimal.
3. Input your data in the field Number in the corresponding numeral system. For our example, we put here $27$.
4. Choose your shifting direction, either Left or Right, to operate the tool as a left shift calculator or right shift calculator. We choose Left.
5. The bit shift calculator presents your result as numbers from the binary, decimal, and octal systems:

• binary: $0110\ 1100$
• octal: $154$
• decimal: $108$

In case your binary result starts with a $1$ and could therefore be interpreted as a positive result in unsigned notation or a negative result in signed notation, both results will be displayed.

Bit shifting describes the operation of shifting a string of bits a certain number of positions to the left or the right. For example, the binary number 0001 0101 shifted 1 bit to the left is 0010 1010.

To calculate a left shift by 3 bits, follow these steps:

1. Get your number in a binary format, e.g., 0000 0101.
2. Shift your bit string 3 positions to the left, discarding the digits falling out of scope, and filling up from the right with 0's: 0010 1000.
3. And that's it; you performed a shift of 3 bits to the left.

A logical bit shift is an operation in which a succession of bits is either shifted to the left or the right by a certain number of positions, and the empty digits of the binary number are filled up with 0's.

To multiply a number by 8 using bit shifts, do the following:

1. Get your number in binary format.
2. Shift your binary number 3 bits to the left.
3. That's it; you performed multiplication by 8 using bit shifts.