Binary Subtraction Calculator

This binary subtraction calculator is a great tool to help you understand how to subtract binary numbers. Here you can find descriptions of the two primary methods that deal with the subtraction of binary numbers, namely the Borrow Method and the Complement Method. There is also a short note about the different representations of signed and unsigned binary numbers at the end.

If you need to add numbers, let's try our binary addition calculator.

The subtraction of binary numbers is essentially the same as for the decimal, hexadecimal, or any other system of numbers.

Just to clarify, binary numbers are values containing only two types of digits, 0 or 1. Every digit refers to the consecutive powers of 2 and whether it should be multiplied by 0 or 1. As an example, 13 in decimal notation is equivalent to 1101 in binary notation, because 13 = 8 + 4 + 1, or 13 = 1×2³ + 1×2² + 0×2¹ + 1×2⁰ using scientific notation. Use binary converter whenever you need to switch between decimal and binary notation.

So, how to subtract binary numbers, e.g., 1101 - 110? We can always convert these values to decimals, classically subtract them, and then transform them once again into the binary form:

1101₂ - 110₂ = 13₁₀ - 6₁₀ = 7₁₀ = 111₂

Here ₂ denotes a binary number, and ₁₀ is a decimal number. As long as the number of digits is relatively small, we can do it by hand. For long numbers, it gets quite tricky. And what if we wanted to subtract a larger number from a smaller one? Here is where the binary subtraction calculator comes in handy! Let's jump to the next section to learn about the different methods of solving these problems.

In this part, we will describe two methods of dealing with the subtraction of binary numbers, the Borrow Method and the Complement Method. There are several other tricks as well, but these two are the most prevalent and help you understand the problem better.

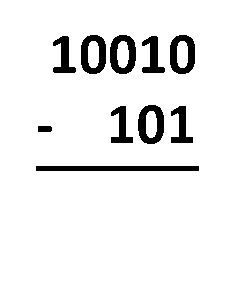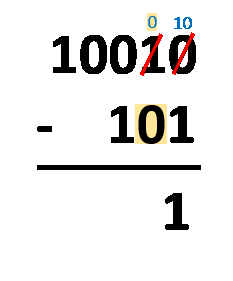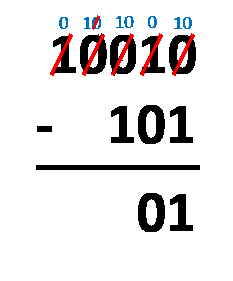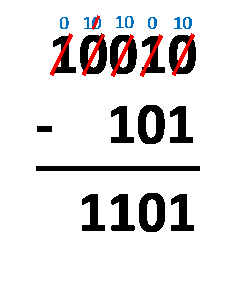
1. Borrow Method – all you have to do is align the numbers as you would do with regular decimal subtraction. The procedure is almost the same! The only difference is that you operate with only two digits, not ten. You need to subtract digits in the same column, following these rules:

   • 1 - 0 = 1;
   • 1 - 1 = 0;
   • 0 - 0 = 0; and
   • 0 - 1 = 1, which actually comes from 10 - 1 = 1, as you borrow 1 from the closest digit to the left, and after all that, the 1 you borrowed becomes 0.

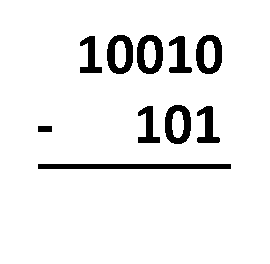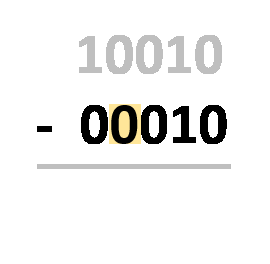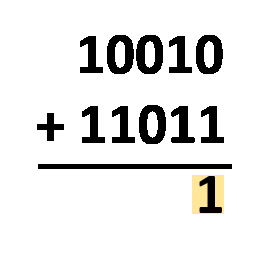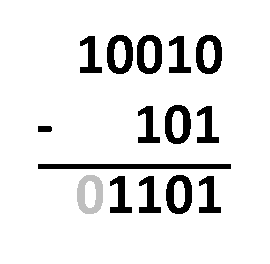
2. Complement Method – the process consists of a few steps:

   • Align the numbers as would normally;
   • Fill the second number with leading 0's so that both values have the same number of digits;
   • Replace the second number with its two's complement;
   • Add these two binary numbers;
   • Remove the leading 1 from the result, as there will be one digit more than we need; and
   • That's it! The remaining part is the final result.

If you want to see a step-by-step solution for your problem using the Complement Method, select "Yes" at the bottom of our binary subtraction calculator. For a more detailed explanation, also check our two's complement calculator.

By the way, did you know that the concept of binary subtraction is quite common in several parts of a developers' toolkit? For example, the chmod command is one of them.

Let's see how to subtract two binary numbers, e.g., 110 0101 - 1000 1100. It's quite tricky because the second number has more digits than the first one, so we are about to subtract a larger number from a smaller one.

There is a clever way to work around this task. We can use the identity a - b = -(b - a), so we're going to reverse the order of subtraction and add a minus sign at the end. In other words, we estimate the absolute value and eventually attach a minus sign. Let's use the complement method:

1. By reversing the order, we have 1000 1100 - 110 0101.

2. Fill the second value with one leading zero, 1000 1100 - 0110 0101.

3. Find the complement of the second number – switch digits (0→1, 1→0) and add 1, 0110 0101 → 1001 1011.

4. Add the first number and the complement of the second one together, 1000 1100 + 1001 1011 = 1 0010 0111.

5. Remove the leading 1 and any adjacent 0's, 1 0010 0111 → 10 0111.

6. Remember to add a minus sign so the outcome becomes -10 0111.

7. The final result of the subtraction of these binary numbers is 110 0101 - 1000 1100 = -10 0111.

8. We can also convert the values to decimals to confirm the computations: 110 0101₂ - 1000 1100₂ = 101₁₀ - 140₁₀ = -39₁₀ = -10 0111₂. Wonderful!

Before making any computation, there is one crucial thing we have to take into account – the representation of numbers in binary code, especially the sign. We'll explain that in the next section.

There are at least three methods:

• Use the minus sign (-) like we usually do with decimal numbers. In the 8-bit code, 5 in binary is 0000 0101, while -5 is -0000 0101.

• Use the first digit as the sign, typically 0 for positive and 1 for negative. Now -5 becomes 1000 0101.

• Represent a negative number as the complement of the positive one, so -5 is now 1111 1011. The first digit still indicates the sign of a number.

Our binary subtraction calculator uses the minus sign, i.e., the 1st method. Whenever you copy a value to our tool, make sure you input the number using the appropriate representation, e.g., if it has the first digit representing the sign, substitute 1 with -, or leave 0 as it is.

There are at least three methods you can use to subtract binary numbers:

• Borrow method – align the numbers and subtract by borrowing as always, remembering that 10 - 1 resolves to 1.
• Complement method – the idea is to replace the subtracted number with its complement and add the two numbers. Remember to omit the leading 1 from the result!
• Conversion method – convert your binary numbers to decimals, subtract, and then transform them back to binary. Effective for small numbers.

To determine the complement of a binary number in the 8-bit system, follow these steps:

1. Make sure your binary has 8 digits. If it has fewer, add some leading zeros.
2. Replace every digit with the opposite one: 0→1 and 1→0.
3. Increase the number by 1. That's it!

101 - 11 = 10. Indeed, using the borrow method, we see the last digit of the result must be 1 - 1 = 0. Then to perform 0 - 1 we need to borrow 1: 0 - 1 = 10 - 1 = 1. And that's it: since we've borrowed, no digits are left. Hence, the result is 10.