Calculadora de resta de binaria

Esta calculadora de resta binaria es una gran herramienta para ayudarte a entender cómo restar números binarios. Aquí encontrarás descripciones de los dos métodos principales que se ocupan de la resta de números binarios, a saber, el Método de la Sustracción y el Método del Complemento. Al final también hay una breve nota sobre las distintas representaciones de los números binarios con y sin signo.

Si necesitas sumar números, probemos nuestra calculadora de sumas binarias 🇺🇸.

La resta de números binarios es esencialmente la misma que la de los números decimales, hexadecimales o de cualquier otro sistema numérico.

Para que quede claro, los números binarios son valores que sólo contienen dos tipos de dígitos, 0 ó 1. Cada dígito hace referencia a las potencias de 2 consecutivas y a si debe multiplicarse por 0 o por 1. Por ejemplo, 13 en notación decimal equivale a 1101 en notación binaria, porque 13 = 8 + 4 + 1, o 13 = 1×2³ + 1×2² + 0×2¹ + 1×2⁰ utilizando la notación científica. Utiliza conversor binario 🇺🇸 siempre que necesites cambiar entre notación decimal y binaria.

Entonces, ¿cómo restar números binarios, por ejemplo, 1101 - 110? Siempre podemos convertir estos valores a decimales, restarlos clásicamente y luego transformarlos de nuevo a su forma binaria:

1101₂ - 110₂ = 13₁₀ - 6₁₀ = 7₁₀ = 111₂

Aquí ₂ denota un número binario, y ₁₀ es un número decimal. Mientras el número de dígitos sea relativamente pequeño, podemos hacerlo a mano. Para números largos, la cosa se complica bastante. ¿Y qué pasa si queremos restar un número mayor de uno menor? ¡Aquí es donde resulta útil la calculadora de resta de binarios! Pasemos al siguiente apartado para conocer los distintos métodos de resolución de estos problemas.

En esta parte, describiremos dos métodos para tratar la resta binaria, el Método del préstamo y el Método del complemento. También existen otros trucos, pero estos dos son los más frecuentes y te ayudarán a comprender mejor el problema.

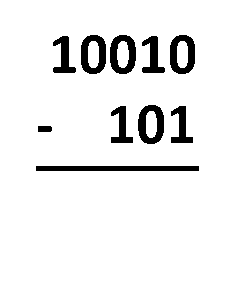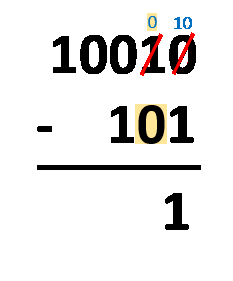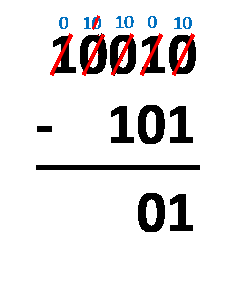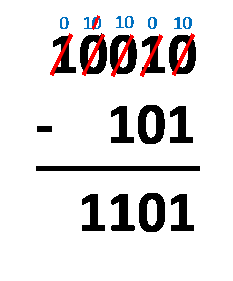
1. Método del préstamo: todo lo que tienes que hacer es alinear los números como harías con la resta decimal típica. ¡El procedimiento es casi el mismo! La única diferencia es que sólo operas con dos dígitos, no con diez. Tienes que restar dígitos en la misma columna, siguiendo estas reglas:

   • 1 - 0 = 1;
   • 1 - 1 = 0;
   • 0 - 0 = 0;
   • 0 - 1 = 1, que en realidad viene de 10 - 1 = 1, ya que tomas prestado 1 del dígito más cercano a la izquierda, y después de todo eso, el 1 que tomaste prestado se convierte en 0.

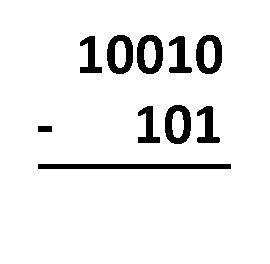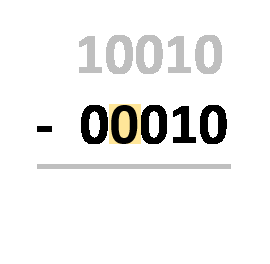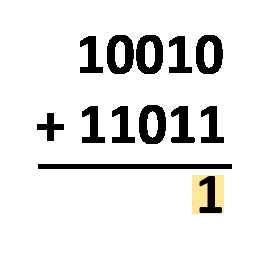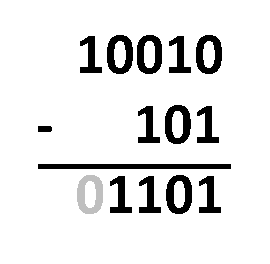
2. Método complementario: el proceso consta de unos pocos pasos:

   • Alinea los números como lo harías normalmente;
   • Rellena el segundo número con "0" a la izquierda para que ambos valores tengan el mismo número de dígitos;
   • Sustituye el segundo número por su complemento a dos;
   • Suma estos dos números binarios;
   • Elimina el 1 inicial del resultado, ya que habrá un dígito más del que necesitamos;
   • Ya está, lo que queda es el resultado final.

Si quieres ver una solución paso a paso de tu problema utilizando el Método del Complemento, selecciona "Sí" en la parte inferior de nuestra calculadora de restas binarias. Para una explicación más detallada, consulta también nuestra calculadora del complemento a dos.

Por cierto, ¿sabías que el concepto de resta binaria es bastante común en la programación y la ingeniería informática? Por ejemplo, el comando chmod es una de ellas.

Veamos cómo restar dos números binarios, por ejemplo, 110 0101 - 1000 1100. Es bastante complicado porque el segundo número tiene más dígitos que el primero, así que estamos a punto de restar un número mayor a uno menor.

Hay una forma inteligente de resolver esta tarea. Podemos utilizar la identidad a - b = -(b - a), así que vamos a invertir el orden de la resta y añadir un signo menos al final. En otras palabras, estimamos el valor absoluto y al final añadimos un signo menos. Utilicemos el método del complemento:

1. Invirtiendo el orden, tenemos 1000 1100 - 110 0101.

2. Rellena el segundo valor con un cero a la izquierda, 1000 1100 - 0110 0101.

3. Encuentra el complemento del segundo número, cambia los dígitos (0→1, 1→0) y suma 1, 0110 0101 → 1001 1011.

4. Suma el primer número y el complemento del segundo, 1000 1100 + 1001 1011 = 1 0010 0111.

5. Elimina el 1 inicial y cualquier 0 adyacente, 1 0010 0111 → 10 0111.

6. Recuerda añadir un signo menos para que el resultado sea -10 0111.

7. El resultado final de la resta de estos números binarios es 110 0101 - 1000 1100 = -10 0111.

8. También podemos convertir los valores a decimales para confirmar los cálculos: 110 0101₂ - 1000 1100₂ = 101₁₀ - 140₁₀ = -39₁₀ = -10 0111₂. ¡Maravilloso!

Antes de realizar cualquier cálculo, hay algo crucial que debemos tener en cuenta: la representación de los números en código binario, especialmente el signo. Lo explicaremos en el siguiente apartado.

Existen al menos tres métodos:

• Utilizar el signo menos (-) como solemos hacer con los números decimales. En el código de 8 bits, 5 en binario es 0000 0101, mientras que -5 es -0000 0101.

• Utiliza el primer dígito como signo, normalmente 0 para positivo y 1 para negativo. Ahora -5 se convierte en 1000 0101.

• Representa un número negativo como el complemento del positivo, así que -5 es ahora 1111 1011. El primer dígito sigue indicando el signo de un número.

Nuestra calculadora de restas binarias utiliza el signo menos, es decir, el 1er método. Siempre que copies un valor en nuestra herramienta, asegúrate de introducir el número utilizando la representación adecuada, por ejemplo, si tiene el primer dígito que representa el signo, sustituye 1 por -, o deja 0 tal cual.

Hay al menos tres métodos que puedes utilizar para restar números binarios:

• Método del préstamo: alinea los números y réstalos como siempre, recordando que 10 - 1 da como resultado 1.
• Método del complemento: la idea es sustituir el número restado por su complemento y sumar los dos números. Recuerda omitir el "1" inicial del resultado
• Método de conversión: convierte tus números binarios en decimales, resta y luego vuelve a transformarlos en binarios. Eficaz para números pequeños.

Para determinar el complemento de un número binario en el sistema de 8 bits, sigue estos pasos:

1. Asegúrate de que tu binario tiene 8 dígitos. Si tiene menos, añade algunos ceros a la izquierda.
2. Sustituye cada dígito por el opuesto: 0→1 y 1→0.
3. Aumenta el número en 1. Ya está

101 - 11 = 10. Efectivamente, utilizando el método del préstamo, vemos que el último dígito del resultado debe ser 1 - 1 = 0. Entonces, para realizar 0 - 1 necesitamos tomar prestado 1: 0 - 1 = 10 - 1 = 1. Y ya está: como hemos tomado prestado, no queda ningún dígito. Por tanto, el resultado es 10.