Binäre Subtraktion Rechner

Dieser Rechner für die Subtraktion von Binärzahlen ist ein großartiges Hilfsmittel, um zu verstehen, wie man Binärzahlen subtrahiert. Hier findest du Beschreibungen der beiden Hauptmethoden, die sich mit der Subtraktion von Binärzahlen befassen – die Borgen-Methode und die Komplement-Methode. Wir geben dir zudem Hinweise auf die unterschiedlichen Darstellungen von Binärzahlen mit und ohne Vorzeichen.

Wenn du Binärzahlen addieren möchtest, probiere unseren Binärrechner Addition aus.

Die Subtraktion von Binärzahlen ist im Grunde genommen dasselbe wie für das Dezimal-, Hexadezimal- oder jedes andere Zahlensystem.

Binäre Zahlen sind Werte, die nur zwei Arten von Ziffern enthalten, 0 oder 1. Jede Ziffer bezieht sich auf die aufeinanderfolgenden Potenzen von 2 und darauf, ob sie mit 0 oder 1 multipliziert werden soll. Ein Beispiel: Die dezimale Schreibweise von 13 entspricht der binären Schreibweise 1101, denn in wissenschaftlicher Schreibweise haben wir 13 = 8 + 4 + 1, oder 13 = 1×2³ + 1×2² + 0×2¹ + 1×2⁰. Verwende den Binärzahlen Umrechner 🇺🇸, wenn du zwischen Dezimal- und Binärschreibweise wechseln musst.

Wie kann man also Binärzahlen subtrahieren, z. B. 1101 - 110? Wir können diese Werte immer in Dezimalzahlen umwandeln, sie klassisch subtrahieren und dann wieder in die binäre Form umwandeln:

1101₂ - 110₂ = 13₁₀ - 6₁₀ = 7₁₀ = 111₂.

Hier steht ₂ für eine Binärzahl und ₁₀ für eine Dezimalzahl. Solange die Anzahl der Ziffern relativ klein ist, können wir das schriftlich machen. Bei großen Zahlen wird es ziemlich knifflig. Und was ist, wenn wir eine größere Zahl von einer kleineren subtrahieren möchten? Hier kommt der Rechner für die binäre Subtraktion ins Spiel! Springen wir zum nächsten Abschnitt, um mehr über die verschiedenen Methoden zum Lösen dieser Probleme zu erfahren.

In diesem Teil werden wir zwei Methoden beschreiben, wie man mit der Subtraktion von Binärzahlen umgeht, die Borgen-Methode und die Komplement-Methode. Es gibt auch noch einige andere Tricks, aber diese beiden sind am weitesten verbreitet und helfen dir, das Problem besser zu verstehen.

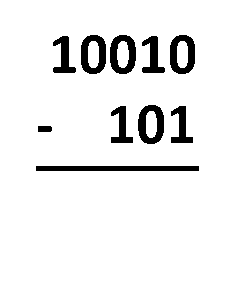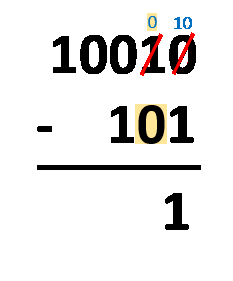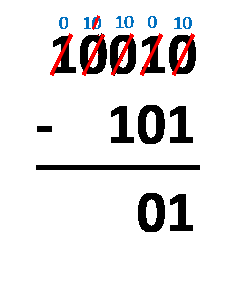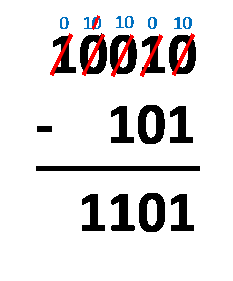
1. Borgen-Methode – du musst die Zahlen nur so untereinander aufschreiben, wie du es bei der normalen Dezimalsubtraktion tun würdest. Der Vorgang ist fast derselbe! Der einzige Unterschied ist, dass du mit nur zwei Ziffern operierst, nicht mit zehn. Du musst die Ziffern in derselben Spalte subtrahieren und dabei diese Regeln befolgen:

   • 1 - 0 = 1;
   • 1 - 1 = 0;
   • 0 - 0 = 0; und
   • 0 - 1 = 1, was eigentlich von 10 - 1 = 1 kommt, da du dir die 1 von der nächstgelegenen Ziffer auf der linken Seite ausborgst und die geborgte 1 dann zu 0 wird.

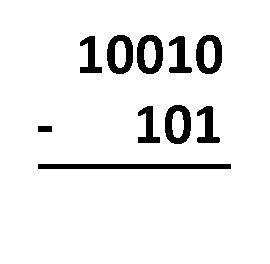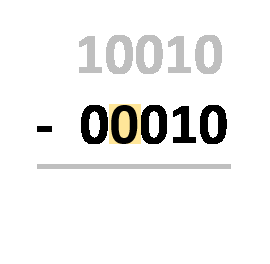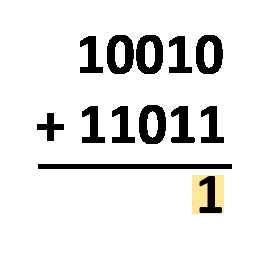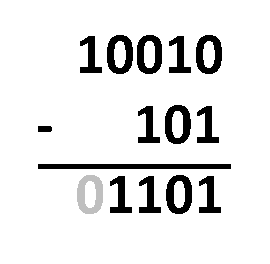
2. Komplement-Methode – der Prozess besteht aus ein paar Schritten:

   • Schreibe die Zahlen wie gewohnt auf;
   • Fülle die zweite Zahl mit führenden Nullen auf, sodass beide Werte die gleiche Anzahl von Ziffern haben;
   • Ersetze die zweite Zahl durch ihr Zwillingskomplement;
   • Addiere diese beiden Binärzahlen;
   • Entferne die führende 1 aus dem Ergebnis, da es eine Ziffer mehr ist, als wir brauchen; und
   • Das war's! Der verbleibende Teil ist das Endergebnis.

Wenn du eine Schritt-für-Schritt-Lösung für dein Problem mit der Komplement-Methode möchtest, wähle unten in unserem Rechner für binäre Subtraktion die Option Ja aus. Eine ausführlichere Erklärung findest du auch in unserem Zweierkomplement Rechner.

Wusstest du, dass das Konzept der binären Subtraktion in mehreren Teilen von Entwickler-Toolkits vorkommt? Der Befehl chmod ist zum Beispiel einer davon.

Schauen wir uns an, wie man zwei Binärzahlen subtrahiert, z. B. 110 0101 - 1000 1100. Das ist ziemlich knifflig, denn die zweite Zahl hat mehr Ziffern als die erste. Wir sind also dabei, eine größere Zahl von einer kleineren zu subtrahieren.

Es gibt einen cleveren Weg, diese Aufgabe zu umgehen. Wir können die Identität a - b = -(b - a) verwenden, also kehren wir die Reihenfolge der Subtraktion um und fügen am Ende ein Minuszeichen hinzu. Mit anderen Worten: Wir schätzen den absoluten Wert und hängen am Ende ein Minuszeichen an. Wenden wir die Komplement-Methode an:

1. Indem wir die Reihenfolge umkehren, erhalten wir 1000 1100 - 110 0101.

2. Fülle den zweiten Wert mit einer führenden Null auf, 1000 1100 - 0110 0101.

3. Finde das Komplement der zweiten Zahl – tausche die Ziffern (0→1, 1→0) und addiere 1, 0110 0101 → 1001 1011.

4. Addiere die erste Zahl und das Komplement der zweiten Zahl zusammen, 1000 1100 + 1001 1011 = 1 0010 0111.

5. Entferne die führende 1 und alle angrenzenden Nullen, 1 0010 0111 → 10 0111.

6. Denke daran, ein Minuszeichen hinzuzufügen, damit das Ergebnis -10 0111 wird.

7. Das Endergebnis der Subtraktion dieser Binärzahlen ist 110 0101 - 1000 1100 = -10 0111.

8. Wir können die Werte auch in Dezimalzahlen umwandeln, um die Berechnungen zu bestätigen: 110 0101₂ - 1000 1100₂ = 101₁₀ - 140₁₀ = -39₁₀ = -10 0111₂. Wunderbar!

Bevor wir eine Berechnung durchführen, müssen wir eine entscheidende Sache beachten – die Darstellung von Zahlen in Binärschreibweise, insbesondere das Vorzeichen. Das werden wir im nächsten Abschnitt erklären.

Es gibt mindestens drei Methoden:

• Verwendet das Minuszeichen (-), wie wir es normalerweise mit Dezimalzahlen machen. Im 8-Bit-Code ist 5 im Binärcode 0000 0101, während -5 -0000 0101 ist.

• Benutze die erste Ziffer als Vorzeichen, normalerweise 0 für positiv und 1 für negativ. -5 wird zu 1000 0101.

• Stelle eine negative Zahl als das Komplement der positiven Zahl dar, -5 ist jetzt somit 1111 1011. Die erste Ziffer gibt immer noch das Vorzeichen einer Zahl an.

Unser Rechner verwendet das Minuszeichen, d. h. die erste Methode. Wenn du einen Wert in unser Tool kopierst, achte darauf, dass du die Zahl in der richtigen Darstellung eingibst, z. B. wenn die erste Ziffer das Vorzeichen darstellt, ersetze 1 durch - oder lass die 0 stehen.

Es gibt mindestens drei Methoden, mit denen du Binärzahlen subtrahieren kannst:

• Borgen-Methode – schreibe die Zahlen wie für die normale schriftliche Subtraktion untereinander auf. Subtrahiere wie immer durch Borgen; beachte dabei, dass 0 - 1 zu 1 aufgelöst wird.
• Komplement-Methode – die subtrahierte Zahl wird durch ihr Komplement ersetzt und die beiden Zahlen werden addiert. Vergiss nicht, die führende 1 aus dem Ergebnis wegzulassen!
• Umwandlungsmethode – wandle deine Binärzahlen in Dezimalzahlen um, subtrahiere und wandle sie dann wieder in Binärzahlen um. Effektiv für kleine Zahlen.

Um das Komplement einer Binärzahl im 8-Bit-System zu bestimmen, gehst du folgendermaßen vor:

1. Stelle sicher, dass deine Binärzahl 8 Ziffern hat. Wenn sie weniger hat, füge die notwendigen führenden Nullen hinzu.
2. Ersetze jede Ziffer durch die gegensätzliche Ziffer: 0→1 und 1→0.
3. Erhöhe die Zahl um 1. So geht's!

101 - 11 = 10. Wenn wir die Borgen-Methode anwenden, sehen wir, dass die letzte Ziffer des Ergebnisses 1 - 1 = 0 sein muss. Um 0 - 1 zu berechnen, müssen wir 1 ausleihen: 0 - 1 = 10 - 1 = 1. Und das war's: Da wir geborgt haben, sind keine Ziffern mehr übrig. Das Ergebnis ist also 10.