Sidereal Time Calculator

Our sidereal time calculator is a comprehensive and clear tool that can help you in your understanding of this apparently complex topic of astronomy and timekeeping. In this article, you will learn:

• What the sidereal time is.
• How do you calculate the Greenwich sidereal time.
• The difference between mean and apparent sidereal time.
• How to calculate the local sidereal time.
• The formulas to calculate the sidereal time.

It may seem advanced, but once the problem's scope is clear, you will see that it's only a matter of formulas! Follow us!

Time is nothing but a way to keep track of another coordinate in our neverending need to define the positions of the objects around us. In astronomy and geography, time assumes a critical connotation. From the earliest days of humanity's astronomical observations and explorations around the globe, determining the position of celestial objects became an ever-increasingly fundamental task, particularly considering that small contributions, initially negligible, slowly became noticeable due to our improvement of measuring tools and models.

The problem we will consider in the sidereal time calculator is that the motion of Earth is rather complex. As it rotates around its axis, our planet orbits around the Sun (we call this movement revolution). Considering that Earth's orbit is almost circular (the eccentricity, which you can calculate at our conic sections calculator, is very small: $0.0167$), we can say that we cover $1\degree$ of the orbit every day. But what is a day?

If the answer to this question was "the time required by the Earth to complete a rotation", we have both good and bad news. This is the correct answer to another question!

A day, in the meaning we use every day is the time that passes between two culminations of the Sun (a culmination is when the Sun is precisely above the Southern cardinal direction). We divide the duration of a day into 24 hours. This quantity, called synodic day, is not the time required to complete a rotation. Look at the image below.

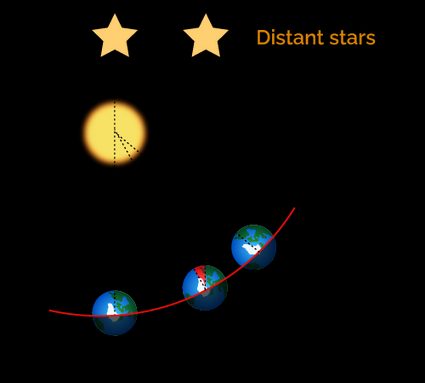
There are two references used to compute the length of a day. One is all the distant stars, or fixed, that never change their position relative to Earth. The other is the Sun. By the time Earth completes a rotation around its axis regarding distant stars, it also moves on its orbit enough that it anticipates the culmination of the Sun by about 4 minutes. After those 4 minutes, the Sun returns to its starting position, and the cycle repeats. This slight difference distinguishes between the synodic and the sidereal day.

A sidereal day is a time required to complete a full rotation of Earth. Its duration is approximately 23 hours, 56 minutes, and 4 seconds. Counting time using this reference gives us the sidereal time.

Sidereal time is a univocal reference for the position of celestial objects in the sky. As it measures the rotation of Earth, we can easily associate it with another angle called right ascension. The sidereal time identifies the position of Earth related to the celestial background. Right ascension is a univocal coordinate that corresponds to the longitude of a celestial body measured from the vernal equinox (the intersection between elliptic, the projection of Earth's orbit in the sky, and the celestial equator, the projection of Earth's equator where we can find the Sun around the 20^th of March).

By subtracting sidereal time and right ascension, we find an object's hour angle, which is an indication of the object's position in the sky related to the observer. When measured in hours, the hour angle tells us if the object is rising, setting, or culminating and quantifies its position.

Calculating the sidereal time is not a complicated task after all. We will follow some simple steps:

1. Convert the UT1 time (universal time) and date to Julian time.
2. Use a formula to find the sidereal time measured in angle.
3. Convert the angle to hours or any time unit.
4. Eventually, consider the effects of nutations (see later on in this text).

Let's see them in detail!

Conversion to Julian time

Julian time is a continuous way to measure time. It's a modification of the Julian date, a count of days from an initial reference date (the 1^st January 4713BC). This method has obvious limitations, but we can easily expand it by adding hours, minutes, and seconds.

To find the Julian date, use the following formula:

where:

In the formulas above, we identify the following:

• $y$ — The year;
• $m$ — The number of the month (with January counted as $1$);
• $d$ — The day of the month.

We need a more accurate measure of time to compute the sidereal time. We introduce hours, minutes, and seconds n the calculations. To calculate the Greenwich mean sidereal time, we use the UT1 time, an accurate measurement of time about the position of distant stars, which differs from UTC (the coordinated universal time) by a variable quantity smaller than 0.8 seconds.

By setting the beginning of a Julian day at midday of UT1, we add the decimal part of the Julian time with the formula:

If the time is before 12 UT1, we assign the time to the previous day's $\mathrm{JDN}$.

The formula to calculate the Greenwich mean sidereal time

Once you know the Juian time, use it to calculate the Greenwich mean sidereal time with the following formula:

where:

• $D_\mathrm{tt} = \mathrm{JDT}-2451545.0$ — where $2451545.0$ is midday of the 1^st January 2000, terrestrial time; and
• $t= D_\mathrm{tt}/36525.0$ — The fraction of the century elapsed since the reference date above.

The result of this equation is in degrees. Thanks to this, we can compute its modulo 360°: every sidereal day corresponds to a complete rotation. By convention, we convert this angle in hours by dividing it by $360/24 = 15$.

The effect of nutation on the calculation of the sidereal time

The previous formula introduced, without much fuss, the dependency of the sidereal time on the precession of the equinox. The precession is the third periodic movement of Earth, a slow (more than 26,000 years long) change of the direction of Earth's axis. You can visualize this movement as a cone in space.

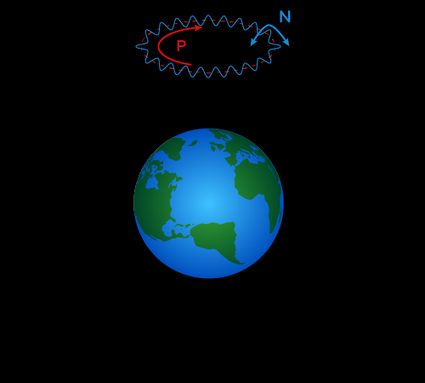
Precession is associated with the gravitational influence of the Sun and Moon on Earth. The same bodies and forces cause another set of movements of much smaller amplitude (the breadth of equinox precession is almost 50°), usually tens of arcseconds, called astronomical nutation of Earth. At the net of precession, these movements would amount to a gentle rotation of the Earth's axis.

Nutation slightly affects the sidereal time, and it is possible that these movements may hinder the determination of the position of a celestial object. We can introduce a small modification to the formula for the GMST that includes the effect of nutation: all we need to do is compute the equation of equinoxes, a correction to the position of the vernal equinox.

Computing the equation of equinoxes ($\rm EoE$) is a tedious procedure where we split the effect of nutation in a longitude component ($\Delta \psi$) and a component for obliquity ($\varepsilon$). You can find all the needed information in the sacred text for the topic, the Explanatory Supplement to the Astronomical Almanac by Seidelmann). The final formula is:

Summing this term to the GMST allows us to find the Greenwich apparent sidereal time, or GAST:

Why did we learn how to calculate the sidereal time for Greenwich? Because as you will see in the next section, this reference position at longitude $0\degree$ is the most often tabulated value. For your astronomical observation, however, you would need to learn how to calculate the local sidereal time, mean, and apparent. Let's do it!

Luckily for us, introducing our position on Earth is not complicated at all: we just need to know our longitude!

Once you know this value, convert it into hours. To do so, if you know it in degrees, minutes, and seconds, follow these steps:

1. Convert your longitude to the range $0\degree$-$360\degree$, going eastward. If you know your longitude as west, subtract it from $360\degree$ to obtain a correct value.
2. Convert the longitude to degrees only: multiply the arcseconds by $3600$ and the seconds by $60$, and sum these results to the number of degrees.
3. Divide this value by $15$ to find the corresponding quantity in hours.

A formula to calculate the sidereal time for your locality simply involves a sum for both the mean and the apparent sidereal times.

For the local mean sidereal time (LMST), we compute:

where $\lambda_\mathrm{h}$ is the longitude expressed in hours.

For the local apparent sidereal time (LAST), we compute a similar formula:

Note how the longitude doesn't matter in these calculations: the only thing affected by your north-south position is your horizon, which is irrelevant while determining the position of a celestial object.

Our calculator is straightforward to use! As you open it, you'll find your local time as the default value. Feel free to change it: you can either select the desired time from the drop-down interface or type in the numbers (use the correct format!). If you input only the time, we will calculate the Greenwich mean and local sidereal time. If you want to calculate the local sidereal time, type your longitude and choose your hemisphere. We will do all the calculations for you!

We created more tools related to the times of our daily lives: visit the sunrise calculator and the sunset calculator to learn how to find the exact time at which our star will cross the horizon!

To calculate the local sidereal time, follow these simple steps:

1. Calculate the Greenwich sidereal time, or find its value in almanac tables.
2. Find your longitude, and convert it in degrees from 0° to 360° measured going eastward.
3. Convert the longitude in hours (divide by 15).
4. Sum the Greenwich sidereal time to the longitude to find the local sidereal time.

The Greenwich mean sidereal time (GMST) and the Greenwich apparent sidereal time (GAST) are closely related concepts. The GAST, however, includes in the computation of the position of Earth compared to distant stars and the minor effects of the Sun and Moon on the orientation of Earth's axis (nutation). To do so, we compute the equation of equinoxes (EoE). The relation between GMST and GAST is as follows:

GAST = GMST + EoE

Stars rise approximately four minutes later every night because we measure time depending on the position of the Sun related to Earth. As Earth orbits its star, the time at which the Sun reaches its maximum height above the horizon (culmination) moves forward (Earth moved forward, and we need to "turn" a bit more to see the Sun in the same position) by approximately four minutes, and drags with its sunrise and sunset, giving us the impression that stars change their rising time.

A sidereal day is approximately 23:56:04 long when measured in hours, minutes, and seconds. This quantity corresponds to a true rotation of Earth when we take as reference the distant stars. The discrepancy of about four minutes from the accepted duration of a day (24 hours) is due to the increased time between two subsequent Sun culminations caused by Earth's motion in its orbit.