Sun Angle Calculator
Welcome to Omni's sun angle calculator, which tells you the Sun's location at any given place on the Earth and time. Read on to learn how to define the Sun's position in the sky and how to calculate Sun's elevation and azimuth angles.
Our solar angle calculator also shows the Sun angles charts for a given date and answers frequently asked questions regarding Sun's altitude.
🔎 If you want to know when the Sun rises and sets, head to our sunrise sunset calculator.
How to define the Sun position in the sky
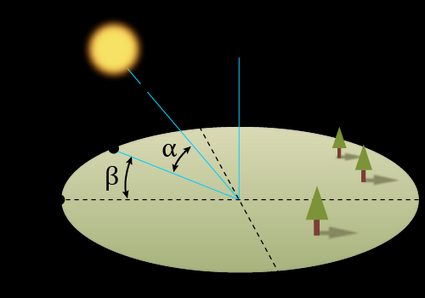
We can express the Sun's location in the sky using two values, imaging it travels on a sphere's surface. Unlike a flat Cartesian plane, it's more convenient to use angles instead of x- and y-coordinates. The most common way to tell someone the Sun's position is to give its elevation and azimuth angles, which closely relate to spherical coordinates. You can read more about them in our spherical coordinates calculator.
Omni's sun angle calculator uses the following convention:
-
The elevation () measures the Sun's height relative to the horizon line. It ranges from -90° to 90°. The positive values denote the Sun is above the horizon, while negative ones mean it's below. The Sun reaches the maximal angle in the zenith – directly above your head.
-
The azimuth () tells you how much you should turn clockwise to look directly at the Sun. The reference direction is usually north, and the azimuth angle spans 0° and 360°. Following this convention, the most common bearings are North (0°), East (90°), South (180°), and West (270°).
🔎 If you need to travel between two points of known coordinates, we recommend using our azimuth calculator so that you can choose the shortest distance.
Where is the Sun right now? The use of the solar angle calculator
Let's say you're in Saint Louis (38.6° N 90.2° W), and it's the 20th of February 2023. The sky is completely overcast, the clock has just hit 3 pm, and you are wondering: “Where is the Sun right now?”. The quickest way to solve the problem is to use Omni's solar angle calculator:
- Type the city's coordinates, 38.6° for latitude and -90.2° for longitude.
- Set the date to 20th of February 2023 and the time to 3 pm.
- Select the time zone based on your location. In our case, it should be CST (UTC-6).
- As a result, you can see that the solar elevation angle equals 27.37°, and the solar azimuth angle is 226.98°. It means that the Sun's location is roughly at a third on the way between the horizon and the zenith and is close to the southwest direction.
💡 The exact values you get from the sun angle calculator may fluctuate a bit from year to year.
- Additionally, you can choose if you want to see any of the Sun angle charts for the selected day at the bottom.
Instead of wondering where the Sun is right now, you may ask at what time the Sun hits the horizon 🌄. Omni's sunset calculator will tell you in a second!
The formulas for solar elevation and azimuth angles – Computing the Sun's location
You can work out the elevation () and azimuth () angles by hand using the following equations:
where:
- — Declination angle;
- — Latitude; and
- — Local hour angle.
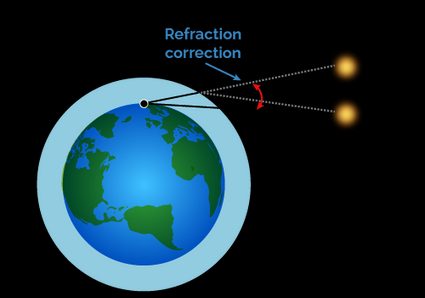
💡 The apparent Sun's elevation differs slightly from the actual one due to the atmospheric refraction effect. Omni's sun calculator returns the apparent Sun's altitude – the one you can actually measure 😎.
The declination is an angle between a vertical line set at the equator and the line connecting Earth's and Sun's centers. Due to Earth's tilt, it varies from -23.45° (at December's solstice) to 23.45° (at June's solstice) and depends on the year's day.
You can estimate Sun's declination for any day of the year using the simplified formula:
Following this equation, you can obtain the declination angle with an accuracy of up to 1° compared to the true value.
The local hour angle depends on the local solar time (). It changes between -180° and 180°, crossing 0° at local noon. The formula for the hour angle is the following:
The unit is hours, and the factor 15° comes from the fact that the Earth makes a 15° rotation during one hour.
🙋 All the formulas presented in this section are approximations. They don't consider additional effects such as the eccentricity of Earth's orbit (due to elliptical orbit) or the precession of the axial tilt. The good news is that we can get precise results using our sun angle calculator!
FAQs
When is the Sun highest in the sky?
During the day, the Sun elevation angle is highest at local noon. There is usually a shift between the solar and official time due to fixed time zones.
During the year, the Sun reaches the zenith for all the locations between the tropics. For other places, it comes to the highest elevation at the summer solstice.
How fast does the Sun move across the sky?
15° per hour. To be precise, it's the Earth that makes a 360° rotation per day, which equals 15° per hour. However, if you measure the azimuth angle (the projectile of the Sun's location), it changes at a different rate depending on your latitude and the date.
How do I calculate the Sun angles?
To estimate the approximate solar elevation and azimuth angles:
-
Get your latitude ϕ.
-
Find the declination angle δ for the given date.
-
Evaluate the hour angle according to the local time T: γ = 15° × (T-12).
-
The elevation angle equals:
α = sin−1[sinδ sinϕ + cosδ cosϕ cosγ].
-
The azimuth angle equals:
β = cos−1[(sinδ cosϕ−cosδ sinϕ cosγ) / cosα],
for negative γ or 360°-β for positive γ.
How does the Sun's path change from season to season?
The Sun's path throughout the year differs depending on the latitude:
-
Between the tropics (ϕ < 23.44°) — It's similar for each day. The Sun reaches zenith twice a year, while the day and night durations are comparable.
-
Middle latitudes (23.44° < ϕ < 66.56°) — The Sun's elevation is highest at the summer solstice and lowest at the winter solstice. In summer, the Sun rises and sets closer to the North azimuth, while in winter, these shift to the South azimuth.
-
Polar (ϕ < 66.56°) – The Sun never sets during the summer (midnight sun) or never rises in winter (polar night). The closer to the poles, the longer these last.