Tank Volume Calculator

Q: How to calculate the volume of a water tank?

You can try the Omni Calculator tool tank volume calculator or do the following: Get the inner radius and the height of the tank . Square the radius, then multiply by pi (3.14159...). Congratulations, you got the water tank area . Multiply the result by the height, and you will obtain the tank volume .

Q: How to calculate the capacity of my engine?

Car experts call it engine displacement, and you can calculate it as follows: Get the volume of one of the cylinders of your engine. You can try the Omni Calculator tool tank volume calculator or get the cylinder radius and height (engine piston stroke). Square the radius, multiply by pi (3.14159...), and then by piston stroke. Multiply the one-cylinder volume by the number of cylinders in your engine, and you will get engine capacity.

Q: How much time can stored water last in a tank?

It will depend on how much water you have stored and the outflow rate. Calculate the volume of your water tank with the Omni Calculator tool tank volume calculator. Get the value in liters. Determine how many liters you consume per day . Divide the amount of water you have by your daily consumption. The result is how many water days you have.

Q: Why we prefer cylindrical water tanks rather than squared?

There are two main reasons why we prefer cylindrical tanks to rectangular tanks: Cylindrical tanks are better at resisting stress than rectangular tanks. Thus, manufacturers require less material to build it. Rectangular tanks are more difficult to clean , specifically in the corners.

Q: What is the volume of an oil barrel?

218.7 liters. An oil barrel has a diameter of 0.572 m and a height of 0.851 m. Plug these figures into the following formula: Volume = π × (d/2)² × h = 3.141 × (0.572/2)² × 0.851 = 0.2187 m² = 218.7 liters

With this tank volume calculator, you can easily estimate the volume of your container. Choose between ten different tank shapes: from standard rectangular and cylindrical tanks to capsule and elliptical tanks. You can even find the volume of a frustum in cone bottom tanks. Just enter the dimensions of your container, and this tool will calculate the total tank volume for you. You may also provide the fill height, which will be used to find the filled volume.

Do you wonder how it does it? Scroll down, and you'll find all the formulas you need – the volume of a capsule tank, elliptical tank, or the widely-used cone bottom tanks (sometimes called conical tanks), as well as many more!

Are you looking for other types of tanks in different shapes and for other applications? Check out our volume calculator to find the volume of the most common three-dimensional solids. For something more specialized, you can also have a glance at the aquarium calculator and pool volume calculators for solutions to everyday volume problems.

How to use the tank volume calculator

This tank volume calculator is a simple tool that helps you find the volume of the tank as well as the volume of the filled part. You can choose between ten tank shapes:

Vertical cylinder;
Horizontal cylinder;
Rectangular prism (box);
Vertical capsule;
Horizontal capsule;
Vertical oval (elliptical);
Horizontal oval (elliptical);
Cone bottom;
Cone top; and
Frustum (truncated cone, funnel-shaped)

"But how do I use this tank volume calculator?", you may be asking. Let's have a look at a simple example:

Decide on the shape. Let's assume that we want to find the volume of a vertical cylinder tank – choose that option from the drop-down list. The schematic picture of the tank will appear below; make sure it's the one you want!
Enter the tank dimensions. In our case, we need to type in the length and diameter. In our example, they are equal to $32\ \mathrm{in}$ and $24\ \mathrm{in}$ , respectively. Additionally, we can enter the filled height – $28\ \mathrm{in}$ .
The tank volume calculator has already found the total and filled volume! The total volume of the tank is $62.7\ \mathrm{US\ gal}$ , and the volume of the liquid inside is $54.8\ \mathrm{US gal}$ . As always, you can change the units by clicking on the volume units themselves. Easy-peasy!

Cylindrical tank volume formula

To calculate the total volume of a cylindrical tank, all we need to know is the cylinder diameter (or radius) and the cylinder height (which may be called length if it's lying horizontally).

Vertical cylinder tank

We may find the total volume of a cylindrical tank with the standard formula for volume – the area of the base multiplied by the height. A circle is the shape of the base, so its area, according to the well-known equation, is equal to $\pi \times \mathrm{radius}^2$ . Therefore the formula for a vertical cylinder tanks volume looks like this:

\begin{split} V_{\scriptsize{\mathrm{\tiny vertical\ cylinder}}} &= \pi \times r^2 \times h\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times h, \end{split}

where:

$r$ — Radius of the base; and
$h$ — Height of the cylinder.

If we want to calculate the filled volume, we need to find the volume of a "shorter" cylinder – it's that easy!

\begin{split} V_{\scriptsize{\mathrm{\tiny vertical\ cylinder}}} &= \pi \times r^2 \times f\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times f, \end{split}

where $f$ is the height of the filled portion of the cylinder.

Horizontal cylinder tank

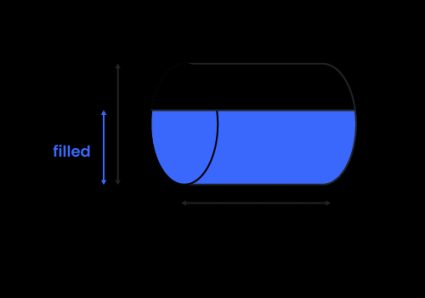
The total volume of a horizontal cylindrical tank may be found in an analogical way – it's the area of the circular end times the length of the cylinder:

\begin{split} V_{\scriptsize{\mathrm{\tiny horizontal\ cylinder}}} &= \pi \times r^2 \times l\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times l, \end{split}

where $l$ is the length of the cylinder.

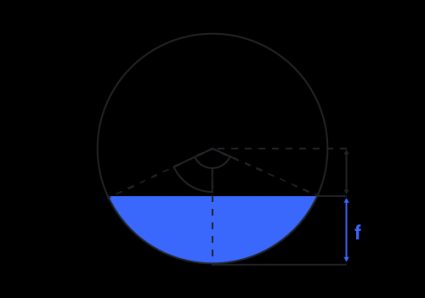
Cross-section of a partially filled cylindrical tank.

Things get more complicated when we want to find the volume of the partially filled horizontal cylinder. First, we need to find the base area: the area of the circular segment covered by the liquid:

A_{\mathrm{\tiny segment}} = \frac{1}{2}\times r^2 \times (\theta-\sin(\theta)),

where $r$ is the radius of the base, and $\theta$ is the central angle of the segment. The angle $\theta$ may be found from the formula for cosine:

\cos\left(\frac{\theta}{2}\right) = \frac{r-f}{f},

where $f$ is the height of the filled section of the base.

Therefore:

\theta= 2\times \arccos\left(\frac{r-f}{f}\right)

And finally, the formula for the volume of a partially filled horizontal cylinder $V_{\scriptsize{\mathrm{fhc}}}$ is:

\small V_{\scriptsize{\mathrm{fhc}}} = 0.5\times r^2\times(\theta -\sin(\theta))\times l,

where:

\theta = 2\times \arccos\left(\frac{r-f}{r}\right)

If the cylinder is more than half full, then it's easier to subtract the empty tank part from the total volume.

Rectangular tank volume calculator (rectangular prism)

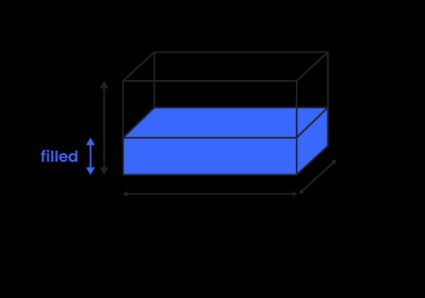
Rectangular tank with marked dimensions.

If you're wondering how to calculate the volume of a rectangular tank (also known as cuboid, box, or rectangular hexahedron), look no further! You may know this tank as a rectangular tank – but that is not its proper name, as a rectangle is a 2D shape, so it doesn't have a volume.

To find the rectangular prism volume, multiply all the dimensions of the tank:

V_{{\mathrm{rectangular\ prism}}} = h\times w\times l,

where:

$h$ — The height of the tank;
$w$ — The width; and
$l$ — The length of the tank.

If you want to know what the volume of the liquid in a tank is, simply change the height variable into filled in the rectangular tank volume formula. The volume of a rectangular filled prism, $V_{\scriptsize{\mathrm{rpf}}}$ , is:

V_{{\mathrm{rpf}}} = f\times w\times l,

where $f$ is the height of the filled portion.

For this tank volume calculator, it doesn't matter if the tank is in a horizontal or vertical position. Just make sure that filled and height are along the same axis.

Formula for volume of a capsule

Our tool defines a capsule as two hemispheres separated by a cylinder. To calculate the total volume of a capsule, all you need to do is add the volume of the sphere to the cylinder part:

V_{\scriptsize{\mathrm{cap}}} = \pi\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\!\times\!\left(\frac{4}{3}\!\times\!\frac{d}{2}\!+\!l\right)

Depending on the position of the tank, the filled volume calculations will differ a bit:

1. For horizontal capsule tank

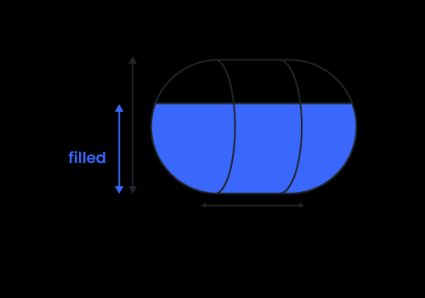
Horizontal capsule tank with marked dimensions.

As the hemispheres on either end of the tank are identical, they form a spherical cap – add this part $V_{\scriptsize{\mathrm{sph\ hf}}}$ to the part from the horizontal cylinder $V_{\scriptsize{\mathrm{fhc}}}$ (check the paragraph above) to calculate the volume of the liquid in a filled horizontal capsule ( $V_{\scriptsize{\mathrm{cap\ hf}}}$ ):

\begin{split} &V_{\scriptsize{\mathrm{cap\ hf}}} = V_{\scriptsize{\mathrm{fhc}}}+V_{\scriptsize{\mathrm{sph\ hf}}}\\[.6em] &= \frac{1}{2}\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\! \times\! (\theta-\sin(\theta))\times l \\[1em] &\quad+\frac{\pi\times f^2}{3}\!\times\!\left(\frac{3}{2}\times d-f\right), \end{split}

where:

$d$ — Diameter of the tank;
$f$ — Filled height; and
$\theta$ — The angle corresponding to the filled sector in the cylinder tank.

2. For vertical capsule tank

The formula differs for various fill heights. In all the next formulas, we will meet these quantities:

$d$ — Diameter of the tank;
$f$ — Height reached by the liquid; and
$l$ — Length of the cylindrical section.

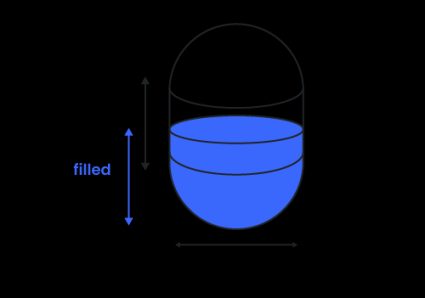
Vertical capsule tank with marked dimensions.

If $f < d/2$ , then the liquid is only in the bottom hemisphere part, so we only need the volume of a spherical cap formula:

\\[2em] V_{\scriptsize{\mathrm{cap\ f}}} = \frac{(\pi\!\times \!f)^2}{3}\!\times\!\left(\frac{3}{2}\!\times \!d - f\right) \\[2em]

If $d/2 < f < d/2 +l$ , then we need to add the hemisphere volume and "shorter" cylinder:

\quad\ \ \ \begin{split} &V_{\scriptsize{\mathrm{cap\ f}}} = \frac{2}{3}\times \pi\left(\frac{d}{2}\right)^3\\[1em] &\qquad+\pi\times\left(\frac{d}{2}\right)^2\times\frac{f-d}{2} \end{split}

If $d/2 + l < f$ , it means that we have a full bottom hemisphere and cylinder, so we just need to subtract the spherical cap (empty part) from the whole volume:

\begin{split} &V_{\scriptsize{\mathrm{cap\ f}}} = V_{\scriptsize{\mathrm{cap}}}\! -\! \frac{\pi\times(l+d-f)^2}{3}\\ &\qquad\ \ \times\left(\frac{3}{2}\times d - (l+d-f)\right) \end{split}

Elliptical tank volume (oval tank)

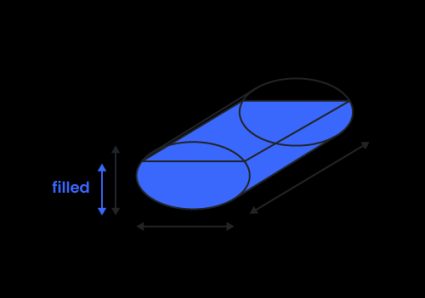
Horizontal oval tank with marked dimensions.

In our calculator, we define an oval tank as a cylindrical tank with an elliptical end (not in the shape of a stadium, as it is sometimes defined). To find the total volume of an elliptical tank, you need to multiply the ellipsis area times the length of the tank:

V_{\scriptsize{\mathrm{ellipse}}} = \pi\!\times\!w\!\times\!l\!\times\!\frac{h}{4},

where:

$w$ — Width of the tank;
$h$ — Height of the tank; and
$l$ — Length of the tank.

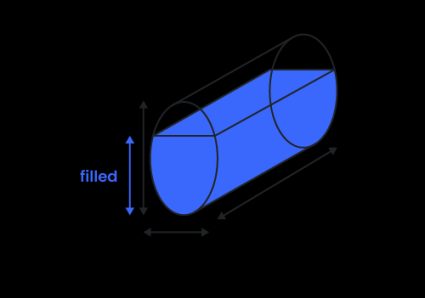
Vertical oval tank with marked dimensions.

Finally, another easy formula! Unfortunately, finding the volume of a partially filled tank – both in the horizontal and vertical positions – is not so straightforward. You need to use the formula for the ellipse segment area and multiply the result times the length of the tank:

\begin{split} &V_{\scriptsize{\mathrm{ell\ f}}} = l\!\times\!h\!\times\!\frac{w}{4}\\[1em] &\qquad\times\!\left[\arccos\left(1\!-\!\frac{2\!\times\!f}{h}\right)\right.\\[1.5em] &\!\!\left.-\!\left(\!1\!-\!\frac{2\!\times\!f}{h}\!\right)\!\times\!\sqrt{\frac{4\!\times\!f}{h}\!-\!\frac{4\!\times\!f^2}{h^2}}\right] \end{split}

Frustum volume – tank in the shape of a truncated cone

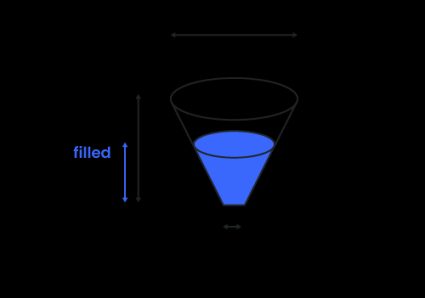
To calculate the truncated cone volume (a particular shape we met at our truncated cone calculator), use the formula:

\begin{split} &V_{\scriptsize{\mathrm{frustum}}} = \frac{1}{3}\times\pi\times h_{\mathrm{cone}}\\[1em] &\qquad\times\left( \left(\frac{d_{\mathrm{top}}}{2}\right)^2\!+\! \frac{d_{\mathrm{top}}}{2}\!\times\!\frac{d_{\mathrm{bot}}}{2}\!\right.\\[1em] &\qquad\qquad \left.+\!\left(\frac{d_{\mathrm{bot}}}{2}\right)^2\right), \end{split}

where:

$d_{\mathrm{top}}$ — Upper diameter of the frustum;
$d_{\mathrm{bot}}$ — Lower diameter of the frustum;
$h_{\mathrm{cone}}$ — Height of the tank.

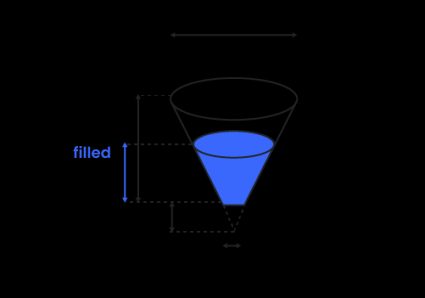
Frustum tank with marked dimensions and liquid level.

If you want to find the partially filled frustum volume for a given fill height, calculate the top radius of the filled part first:

R = \frac{1}{2} \times d_{\mathrm{top}}\times \frac{f+z}{h_{\mathrm{cone}}+z},

where:

z = h_\mathrm{cone} \times \frac{d_{\mathrm{bot}}}{d_{\mathrm{top}}-d_{\mathrm{bot}}}

(You can derive the formula from triangles' similarity.)

Afterward, just find the new frustum volume:

\begin{split} &V_{\scriptsize{\mathrm{ff}}}=\frac{1}{3} \times \pi \times f \\ &\ \ \times \!\left(R^2 \!+ \!R\! \times \!\frac{d_{\mathrm{bot}}}{2} + \left(\frac{d_{\mathrm{bot}}}{2}\right)^2\right) \end{split}

Cone bottom tank volume (conical tank) and cone top tanks

Cone bottom tank with marked dimensions.

Finding the total volume of a cone bottom tank is not so hard – just add the volume of the frustum part to the volume of the cylindrical part:

\begin{split} &V_{\scriptsize{\mathrm{cone\ b}}} = V_{\scriptsize{\mathrm{frustum}}} + V_{\scriptsize{\mathrm{cylinder}}}\\[1em] & =\frac{1}{3}\times\pi\times h_{\mathrm{cone}} \times\left( \left(\frac{d_{\mathrm{top}}}{2}\right)^2\right.\\[1.4em] &\qquad \left.+ \frac{d_{\mathrm{top}}}{2}\!\times\!\frac{d_{\mathrm{bot}}}{2}\!+\!\left(\frac{d_{\mathrm{bot}}}{2}\right)^2\right)\\[1.4em] &\qquad+\pi\times\left(\frac{d_{\mathrm{top}}}{2}\right)^2\times h_{\mathrm{cylinder}}, \end{split}

where:

$d_{\mathrm{top}}$ — Upper diameter of the frustum;
$d_{\mathrm{bot}}$ — Lower diameter of the frustum;
$h_{\mathrm{cone}}$ and $h_{\mathrm{cylinder}}$ — The heights of the two tanks.

To calculate the partially filled tank, just add together the frustum part and cylinder part, depending on the level of the filled liquid, using the equations above.

Calculating the total volume of the cone top tank is exactly the same as the cone bottom tank. The only difference is when you want to find the filled part – of course, firstly, the cylindrical part is filled, and only then the frustum.

🙋 Did you calculate all your volumes using metric units, but you need imperial ones? Worry not, as Omni has a handy solution to all your needs: use our volume conversion tool to quickly convert between volume units!

FAQs

How to calculate the volume of a water tank?

You can try the Omni Calculator tool tank volume calculator or do the following:

Get the inner radius and the height of the tank.
Square the radius, then multiply by pi (3.14159...). Congratulations, you got the water tank area.
Multiply the result by the height, and you will obtain the tank volume.

How to calculate the capacity of my engine?

Car experts call it engine displacement, and you can calculate it as follows:

Get the volume of one of the cylinders of your engine. You can try the Omni Calculator tool tank volume calculator or get the cylinder radius and height (engine piston stroke).
Square the radius, multiply by pi (3.14159...), and then by piston stroke.
Multiply the one-cylinder volume by the number of cylinders in your engine, and you will get engine capacity.

How much time can stored water last in a tank?

It will depend on how much water you have stored and the outflow rate.

Calculate the volume of your water tank with the Omni Calculator tool tank volume calculator. Get the value in liters.
Determine how many liters you consume per day.
Divide the amount of water you have by your daily consumption. The result is how many water days you have.

Why we prefer cylindrical water tanks rather than squared?

There are two main reasons why we prefer cylindrical tanks to rectangular tanks:

Cylindrical tanks are better at resisting stress than rectangular tanks. Thus, manufacturers require less material to build it.
Rectangular tanks are more difficult to clean, specifically in the corners.

What is the volume of an oil barrel?

218.7 liters. An oil barrel has a diameter of 0.572 m and a height of 0.851 m. Plug these figures into the following formula:

Volume = π × (d/2)² × h = 3.141 × (0.572/2)² × 0.851 = 0.2187 m² = 218.7 liters

Tank Volume Calculator

Hanna Pamuła

How to use the tank volume calculator

Cylindrical tank volume formula

Rectangular tank volume calculator (rectangular prism)

Formula for volume of a capsule

Elliptical tank volume (oval tank)

Frustum volume – tank in the shape of a truncated cone

Cone bottom tank volume (conical tank) and cone top tanks

How to calculate the volume of a water tank?

How to calculate the capacity of my engine?

How much time can stored water last in a tank?

Why we prefer cylindrical water tanks rather than squared?

What is the volume of an oil barrel?

Dimensions

Volume