Last updated: Jul 26, 2024

Truncated Cone Calculator

Q: What is a truncated cone in geometry?

A truncated cone is a cone with the apex cut off . Importantly, the cutting plane is parallel to the base , or, equivalently, perpendicular to the height. This solid is also known under the name frustum . In everyday life, you can see truncated cones looking at, e.g., lamp shades.

Q: What is the slant height of a truncated cone with height 4 and radii 1 and 4?

The answer is 5. The slant height formula reads: s = √((R - r)² + h²) . Plugging in our data, we get: s = √((4 - 1)² + 4²) = √25 = 5 .

Q: How do I get the slant height formula for a truncated cone?

Use the Pythagorean theorem to derive the slant height formula. The slant height is the hypotenuse . One of the legs is the difference between the longer and the shorter radius of the truncated cone. The other leg is the height of the truncated cone.

Q: How do I calculate the lateral surface area of a truncated cone with slant height 4?

You need to know the radii to find the area. If the radii are 10 and 12 , then the lateral surface area is 276.46 . To derive this answer: Add together the radii: 10 + 12 = 22 . Multiply the result by the slant height: 22 × 4 = 88 . Multiply by π : 88π ≈ 276.46 . Remember to include the units : if the dimensions are in cm, then the answer is 276.46 cm².

Created by Anna Szczepanek, PhD

Anna Szczepanek

PhD, Jagiellonian University in Kraków, Poland

Website

Holds a Ph.D. degree in mathematics obtained at Jagiellonian University. An active researcher in the field of quantum information and a lecturer with 8+ years of teaching experience. Passionate about everything connected with maths in particular and science in general. Fond of coding, she has a keen eye for detail and perfectionistic leanings. A bookworm, an avid language learner, and a sluggish hiker. She is hopelessly addicted to coffee & chocolate – the darker and bitterer, the better. See full profile

Check our editorial policy

Reviewed by Komal Rafay

Komal Rafay

A master's in Bioinformatics, with 3+ years of experience as a project manager. She has a vast experience of 7+ years in teaching Math, Computer science, and General Sciences, not only professionally but also to help out the children of the neighborhood. She is an enthusiastic reader with a thirst for knowledge who would even read the shampoo labels. As a side hustle that satisfies her love for art, she is a body art and henna expert. In her free time, you will find her reading books, writing short stories, playing with her pets, or experimenting with food while listening to some bouncy music. See full profile

Check our editorial policy

New

Table of contents

What is a truncated cone in geometry?Truncated cone formulas How to use this truncated cone calculator?Related Omni calculators FAQs

This truncated cone calculator is a comprehensive tool for solving various problems related to truncated cones. Our tool will teach you how to find the surface area of a truncated cone: both the lateral area and the total area. Of course, it can compute the slant height and the volume as well. Its best feature though is that it can work in reverse: input whatever data you have and get the missing measurements. No more crying over truncated cones in geometry class. Enjoy!

What is a truncated cone in geometry?

A truncated cone is a cone with the apex cut off. Importantly, the cutting plane is parallel to the base, or, equivalently, perpendicular to the height. This solid is also known under the name frustum. In everyday life, you can see truncated cones looking at, e.g., lamp shades.

Now, let's move on to discussing truncated cone formulas.

Truncated cone formulas

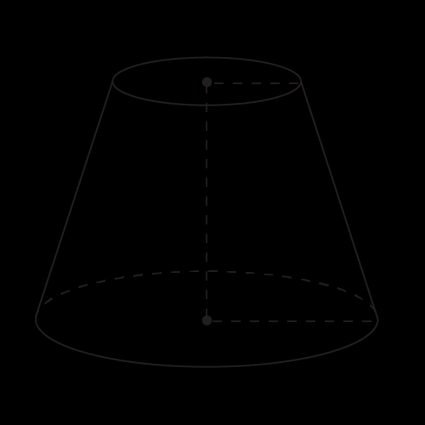
First, we need to establish some notation. Look at the picture below. We have:

R for the radius of the base (larger circle);
r for the radius of the top surface (smaller circle);
h for the height, i.e., the shortest perpendicular distance between the two circles; and
s for the slant height, i.e., the distance between the two circles measured along the lateral face.

Volume formula:

V = (1/3) × π × h × (r² + r × R + R²).

Slant height formula:

s = √((R - r)² + h²).

Lateral surface area formula:

Lateral = π × (R + r) × s.

Top and bottom surface area:

Top = π × r² and Bottom = π × R².

Total area formula:

Total = Lateral + Top + Bottom.

Wow, that's a lot of formulas. But hey, you don't need to learn them by heart! We've implemented them in our truncated cone calculator to save your time and effort.

How to use this truncated cone calculator?

To use this truncated cone calculator, you only need to enter the data: the remaining fields will get calculated immediately. Note that you can adjust the units to your needs!

Did you get a red warning? This means the data you entered is contradictory - please check it carefully and correct any mistakes.

FAQs

What is the slant height of a truncated cone with height 4 and radii 1 and 4?

The answer is 5. The slant height formula reads:

s = √((R - r)² + h²).

Plugging in our data, we get:

s = √((4 - 1)² + 4²) = √25 = 5.

How do I get the slant height formula for a truncated cone?

Use the Pythagorean theorem to derive the slant height formula. The slant height is the hypotenuse. One of the legs is the difference between the longer and the shorter radius of the truncated cone. The other leg is the height of the truncated cone.

How do I calculate the lateral surface area of a truncated cone with slant height 4?

You need to know the radii to find the area. If the radii are 10 and 12, then the lateral surface area is 276.46. To derive this answer:

Add together the radii: 10 + 12 = 22.
Multiply the result by the slant height: 22 × 4 = 88.
Multiply by π: 88π ≈ 276.46.
Remember to include the units: if the dimensions are in cm, then the answer is 276.46 cm².