Miter Angle Calculator

This miter angle calculator, which also works as a miter cut calculator and miter angle finder, will help you determine the angle you would need to set on your miter saw to produce precisely angled crosscuts for your miter joints.

In this calculator, you will learn:

• What a miter cut is;
• How to calculate miter angles using trigonometry; and
• How to determine miter cut angles using the concept of complementary angles.

You can also check our miter saw angle chart, your number one tool to show you how to measure miter cuts. By the end of this text, you will be cutting crown molding miter angles, mitered frames, and so much more with the correct miter saw angles.

In woodworking, a miter is a joint made by crosscutting two pieces of boards at an angle (or two different angles) to form a corner at a specific joint angle. We see miter joints at the corners of a picture frame, crown moldings, and some steel pipe joints and roof trusses.

Finishing a joint with a miter is a simple way of showcasing your woodworking skills with its sophisticated look. We can also see miter joints on some wainscoting and framing designs.

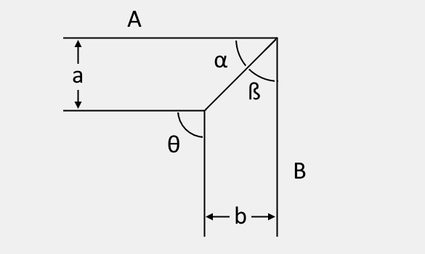
A miter angle is an angle in which we cut a board so that, when joined to another cut board, we form the angled corner we desire. Imagine the four corners of a rectangular picture frame. Each corner is at 90° with pairs of 45° miter angles, as shown in the image below:

For miter joints comprised of boards of the same widths, like in the picture frame shown above, the miter angle is simply half of the joint angle. This means that a joint angle of 120° would need boards cut at 60° to form the corner correctly. However, the process of miter-joining boards of different widths is a different case. In that case, we need more help from trigonometry. In the next section, let us discuss how to calculate miter angles using various trigonometric functions.

In the previous section, we learned that we could find miter cut angles for boards of the same width to be half of the corner's angle (or joint angle) that we denote in this miter angle calculator by the Greek symbol theta, θ. In equation form, we can express the miter angle of boards with equal widths by:

miter angle of each board = θ / 2

For boards of different widths at a 90° joint angle, we need to utilize the trigonometric function arctangent to determine the two angles for both boards. First, we need to measure the width of both boards and substitute their values to the equations below:

board A miter angle = arctan(a / b), and

board B miter angle = arctan(b / a)

where:

• a — the width of board A; and
• b — the width of board B.

To determine the miter angles of boards of different widths at any joint angle other than 90°, we need to use a different pair of equations. These equations are derived using the various trigonometric functions and the properties of right triangles formed within the miter joints. Without showing you their derivations, here are the formulas we use:

narrower board miter angle = arctan(n × sinθ / (m + n × cosθ))

wider board miter angle = θ − narrower board miter angle

where:

• n — the width of the narrower board;
• m — the width of the wider board; and
• θ — the joint angle, as always.

As an exercise, let us consider finding the miter angles of two boards with widths of 10 cm and 15 cm, joined at an angle θ of 120°, as shown below:

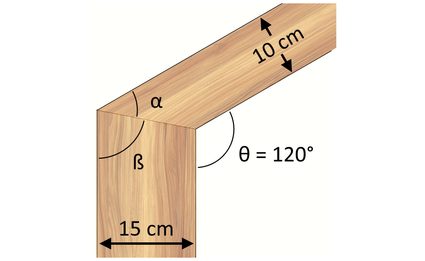
Since we have a miter joint that is not at a 90-degree angle, and the board widths are of different sizes (10 cm for the narrower board, n, and 15 cm for the wider board, m), we will be using the last two formulas in the previous section. Substituting the known values to the first formula, we can calculate the miter angle of the narrower board, α, as follows:

α = arctan(n × sinθ / (m + n × cosθ))

α = arctan(10 cm × sin(120°) / (15 cm + 10 cm × cos(120°)))

α = arctan(10 × 0.8660254038 / (15 + 10 × (- 0.5)))

α = arctan(8.660254038 / 10)

α = 40.89339465° ≈ 40.89°

By subtracting angle α from the total joint angle θ of 120°, we can calculate the miter angle of the wider board, ß, as follows:

ß = θ − α

ß = 120° − 40.89339465°

ß = 79.10660535° ≈ 79.11°

The calculations above show us the miter angles we need to make a perfectly fitting 120° joint angle. If you are going to use a miter saw to cut your boards, keep reading to learn how to properly set up your miter saw angle to cut your boards at any angle you desire.

A miter saw is a tool made specifically to cut miter angles. It is a power tool that allows its cutting blade to be set at an angle, measured by protractors. A miter saw is usually set at a base angle of 0° to cut perpendicularly across a board, which is a cut angle of 90­°, as shown in the image below:

With this idea, we can say that to cut a board at a certain miter angle, we have to set our miter saw angle at the miter angle's complementary angle, and we can calculate it using a simple formula:

miter saw angle = |90° − miter angle|

For our previous example, for us to cut the miter angle 79.11° on the wider board, we have to set our miter saw to be at an angle of 90° − 79.11° = 10.89°. You might also notice that we have included the absolute value symbol in the equation. That is because there are times when the miter angles go above 90°. In those cases, we have to set the miter saw angle towards the other side of the miter saw's protractor.

Another easy miter angle finder is the miter saw angle chart below. There are two sections of the miter saw angle chart — the section for acute miter cut angles and the section for obtuse miter cut angles.

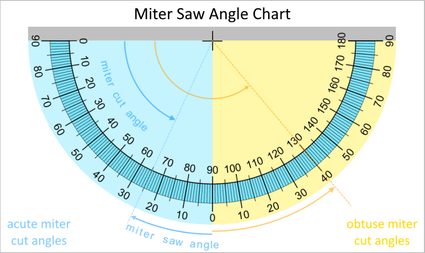
To use the chart, simply follow the inner protractor reading to find your required angle cut, then look at the equivalent outer protractor reading to find the corresponding miter saw angle. You can also use this chart in reverse to measure miter cuts when given the miter saw angle.

If you found this calculator useful and interesting, perhaps you would also like to explore other trigonometric equations or laws by checking out our law of sines calculator and our law of cosines calculator.