Bowl Segment Calculator

With this bowl segment calculator, find the proper measurement and angles to cut your wooden boards to create stunningly beautiful bowls out of wood-turning segments.

Having excellent skills in woodworking always comes with adept control over the numbers and measurements involved in a project. With a tool like this bowl segment calculator, you can concentrate on your craft while we help you with the math.

Keep reading to explore the following topics about the fantastic craft of segmented wood bowl turning:

• What segmented wood turning is;
• How to use this bowl segment calculator;
• How to perform segmented wood bowl calculations; and
• Some frequently asked questions about segmented wood bowls.

From the word "segment," we focus on cutting wood pieces that we glue together to form a ring. We then assemble multiple sets of these rings that we can stack and glue together to create a rough shape of a bowl.

Putting these rings together with a solid bowl base, we can then fix our assembly onto a lathe for turning to carve it into shape.

The outcome is what we then call a segmented wood bowl, as we can see an example of in the image below:

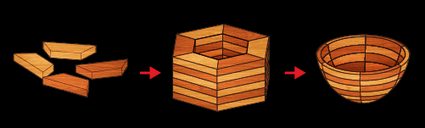
In the next section of this text, let's learn how to use this bowl segment calculator so you can go ahead and begin building your first (if you're new to this) segmented bowl.

This bowl segment calculator is very straightforward and only requires a few pieces of information about your desired segmented bowl. Follow these steps to make the most out of our tool:

1. Enter your preferred number of segments for each bowl ring. Please note that you can only enter at least three segments. On the other hand, choosing to make segmented bowls with more segments will require you to cut tiny pieces of wood segments, which can be challenging to manage.

2. Input your target bowl's outer radius and bowl or ring thickness. You may also enter your desired bowl's inner ring radius. You may prefer to enter the outer diameter and inner diameter of the bowl you want to make. You can enter the Advanced mode or our tool to enter those values.

3. If you're new to turning segmented wood bowls and fear that you might carve too deep on your wood segments, adding allowances to your segment's thickness will help. For that, you can enter the amount of fudge factor for either the inner or outer side of your segments or both.

At this moment, you can already expect our tool to display the dimensions of your wood segments, which includes the length of both the inner and outer sides of your segments, their required thickness, and the cutting angle you'll need to set your protractor or your miter saw at.

Note that you'll have to use our segmented bowl calculator a couple or more times for the different layers of your segmented bowl, especially if your bowl changes in diameter throughout its structure.

And that's it! You can also use our tool in its Advanced mode to display or input other helpful information about your bowl, like the inner and outer circumferences of your segmented bowl's layer.

We powered our bowl segment calculator with equations that work behind the scenes to help you with your segmented wood bowl calculations. In this section, we'll discuss each of them briefly so you can do the computations yourself if you want to.

We start by determining the projected interior angle, $\theta$, of your segments by dividing a full circle by the number of segments, $n$, that you wish to make, as we can see in the equation below:

Utilizing the alternate interior angles theorem, we can conclude that our cutting angle, $\alpha$, is equal to half the interior angle, which leads us to the following equation:

We should set our miter saw or cutting jig so that we'll cut at that angle. Speaking of miters, our cutting angle is also equivalent to the miter angle of two adjacent bowl angles. You can learn more about miters in our miter angle calculator.

From here, we can also use the cutting angle and some trigonometry concepts to find the outer length of our segment with the following formula:

where:

• $L_\text{o}$ — Segment's outer length;
• $R_\text{o}$ — Outer radius of the desired bowl; and
• $a_\text{o}$ — Outer allowance or outer fudge factor.

Then, we use the following equation to determine the segment's inner length:

where:

• $L_\text{i}$ — Segment's inner length;
• $R_\text{i}$ — Inner radius of the desired bowl; and
• $a_\text{i}$ — Inner allowance or inner fudge factor.

It's also nice to remember the relationship between the outside and inside radii with an equation like this one:

where:

• $T_\text{r}$ — Finished ring or bowl thickness.

Finally, to complete our needed segments' dimensions, we need to find the thickness of our segments, $T_\text{s}$. This measurement will help us choose the board we need to use to cut our segments. Here is the formula for that:

If you prefer calculating the dimensions of your bowl segments using the inner and outer diameters of your target bowl, you can replace $R_\text{i}$ and $R_\text{o}$ in our equations by $D_\text{i}/2$ and $D_\text{o}/2$, respectively.

We can also find the inner and outer circumferences of the layers of our segmented bowl by multiplying the outer and inner diameters by the constant pi, respectively.

The formula for segmented wood bowls is as follows:

α = 180° / n

where:

• α — Cutting angle; and
• n — Number of segments.

After which, we can find our segments' longer length (without any allowances) using the following simplified formula:

L = D × tan(α)

where:

• L — Outer length of the segments; and
• D — Outer diameter of your target segmented bowl.

The cutting angle for the segments to make a segmented wood bowl with 9 segments is 20°. We get that value by dividing 180° by the number of segments, which in this case is 9, to have the following: 180° / 9 = 20°.

To find the bowl segment thickness to make a segmented wood bowl with a finished outer diameter of 10 inches (or outer radius of 5 inches) and a bowl thickness of 0.5 inches using 8 segments:

1. First, we divide 180° by 8 segments to get:

   180° / 8 = 22.5°

2. Then we take the inner radius of our finished bowl to be:

   5 inches − 0.5 inches = 4.5 inches

3. Finally, we use the following equation to find the minimum segment thickness we need as follows:

   thickness = outer radius − cos(α) × inner radius

   thickness = 5 inches − cos(22.5°) × 4.5 inches

   thickness = 0.843 inches

Dining bowls typically measure around 9-10 inches in diameter. However, we can also see bowls as small as 6 inches in diameter up to as large as 13 inches in diameter or larger for serving bowls.