Angle Cut Calculator
This angle cut calculator, or woodworking angle finder, will help you determine the dimensions of angled planks used as knee bracing for your framing projects. In this calculator, you will learn what knee bracing is in structures and how to cut wood at an angle for bracing purposes.
Knowing how to calculate angle cuts and using basic algebra and trigonometry are great things to learn, even if you already know how to measure angle cuts in wood using a protractor.
This calculator will help you start cutting angles for tightly fitting knee bracings in no time. Although we focus on knee bracing applications in woodwork, you can also use knee bracings in steel structures. Keep on reading to get started!
What is a knee bracing in structures?
A knee bracing is a diagonal structural member that supports two members, like a column and a beam or a wall and a floor, usually at a perpendicular angle. The neatest way to install a knee bracing is by cutting the ends of the bracing material at certain angles so that one of its ends' surfaces meets the side of the vertical member and the other end meets the surface of the horizontal member.
In the image below, you'll see a post and beam structure with knee bracings installed for additional support, possibly because of beam deflection. You can read through our beam deflection calculator to expand your knowledge about it.

In certain situations, we need to specify the correct angled cuts for the ends of our bracing material to fit perfectly. We can determine these angles using some basic woodworking tools. We can also use some trigonometry equations to calculate the cutting angles and any other related measurements.
🙋 If you want to learn more about wood beams and how to choose the correct wood species, grade, and size so you can avoid the need for knee bracings, you can check out our wood beam span calculator.
How to calculate angle cuts?
When installing knee bracings, you may encounter many different situations that will lead to different starting points for your calculations. But don't worry; we will only need a few basic trigonometry concepts that work regardless of your starting point.
We also need to know the thickness of your plank or bracing material. This thickness should be consistent throughout the entire length of the plank. Once that is all set, we can now proceed to some of the different situations we can encounter.
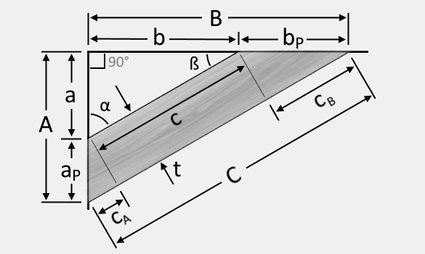
If you have a limited space to place your knee bracing, determine this space's measurements first and use it to calculate the length of bracing you will need. Using the hypotenuse formula, which is based on the Pythagorean theorem, we can find the outer length of our knee bracing as follows:
where:
- – The outer length of our knee bracing;
- – The vertical measurement from where the post and beam intersect to the tip of the knee bracing attached to the post; and
- – The horizontal measurement from where the post and beam intersect to the tip of the knee bracing attached to the beam.
This formula can be used to solve the inner length of the knee bracing, too, if you know the inner measurements of the space you have. We can also utilize the Pythagorean theorem to solve for either length or length if we set a specific outer length for our knee bracing.
After finding the lengths , , and , or just any two of these lengths, we can also determine the angle cuts and using the inverse of the sine, cosine, or the tangent formulas.
Let us jump straight into an example to better understand how to use these formulas.
Finding the cutting angles sample calculation
Let's say we need to install additional knee bracing supports 40 centimeters from the beam of an open shed framing, as shown below:

If we need to use as much of 60-centimeter long and 10 cm wide planks as possible for our knee bracings, we can find the angle cuts by considering the right triangle formed by the open shade framing and our other known measurements, as shown below:
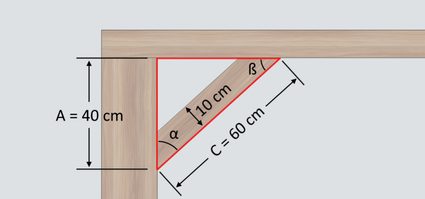
Using the given measurement values, we can calculate angle α using the trigonometric function of arccosine as follows:
Due to the nature of the right triangles, we can easily calculate the value of by finding the complementary angle of :
If you do not have a protractor in your workshop, here is another method on how to cut wood at an angle. You can use the cutting angles and to determine other knee bracing measurements and mark them accordingly before cutting. By considering the illustration below showing the similar right triangles within the knee bracing, you can then mark where to cut on your plank:
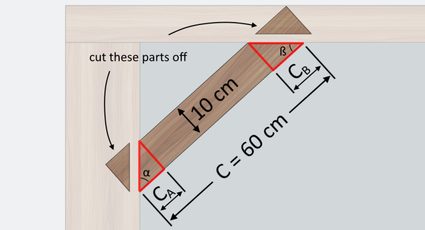
We can calculate the values of small right triangle sides, and , using the trigonometric function tangent and the thickness of the plank, as shown below:
Now that we've determined all the details of our knee bracings, we can now cut the planks and install them afterward.
🙋 Wait! If you plan to butt your knee bracings' ends on the surface of the post and beam, you can go ahead and cut those ends. However, if you plan to use mortise and tenon for your joints, make sure only to mark off these ends and cut only portions of them to leave your desired mortise.
Using our angle cut calculator
From our example above, you can instantly determine the various dimensions and measurements of the knee bracing by entering the given values of plank thickness, length , and length in our angle cut calculator.
To properly use our calculator, make sure you enter the plank thickness (necessary) and any other two known measurements to find the unknown measurements. For best results, refresh the calculator when trying a new set of values.
Apart from knee bracings in wood and knee bracing in steel structures, you can also use our angle cut calculator for roof trusses and when installing supports for the formworks of retaining walls. You can learn more about roof trusses and retaining walls in our roof truss calculator and our retaining wall calculator
Want to learn more?
If you want to learn more about cutting boards and planks at an angle, perhaps you would like to check out our miter angle calculator. In our miter angle calculator (which is another woodworking angle finder), you will learn about what miter cut angle is, how it is different from miter saw angle, and so much more.
FAQs
What is an angle cut?
Angle cut refers to the angle needed to position a miter saw to cut wood into the desired number of sides. Cutting angles are most often used in the process of joining two or more pieces of wood, such as in carpentry.
Which tools are used to cut wood at an angle?
You have a choice of several different tools that allow you to accurately and easily cut angles in wood:
- Miter saw;
- Table saw;
- Compound miter saw;
- Jigsaw;
- Circular saw; and
- Handsaw.
In general, power tools give more accurate angle cuts than a handsaw.
How can I cut 45 degree angle with miter saw?
You can make a 45-degree angle cut on a miter saw by following these steps:
- Prepare the workspace and your miter saw.
- Take a piece of wood, measure the line cut on the wood, and then draw a line.
- Lean the long end of the board against the saw's fence.
- Set the angle of the blade to 45 degrees.
- Turn on the miter saw and cut the wood.
In carpentry, what term means to cut a sloping angle that is not 90 degrees?
"Bevel" means in carpentry an edge cut at an angle other than 90 degrees, usually slopping. It tends to be more difficult and decorative than cutting at 45 degrees. The angle of a bevel cut ranges from a few degrees to 45 degrees and can be adjusted to achieve different shapes and angles.