Venn Diagram Calculator
The Venn diagram calculator is a comprehensive tool that lets you compute all the relevant quantities in two and three-set Venn diagrams. Even though we learn to deal with sets from a young age, set theory is a complex branch of math — keep reading this article to learn:
- What Venn diagrams are;
- How to calculate Venn diagrams, with calculations for 2-circle Venn diagram and 3-circles (shading calculator and numerical calculations); and
- How hard is it to calculate a 4-circle Venn diagram?
How to use our Venn diagram calculator
The following instructions will guide you through our Venn diagram calculator, helping you find the cardinality you desire:
-
Select the number of sets. You can choose either 2 or 3 sets.
-
Input the cardinality (or size) of the universal set |U|.
-
Enter the sets' cardinalities (or sizes), |A| and |B|. If you picked three sets, input the size for the third set |C| as well.
-
Provide the size of any one of the following set relations:
- A excluding B, |A\B|.
- B excluding A, |B\A|.
- A union B, |A∪B|.
- A intersecting B, |A∩B|.
- A XOR B (exclusively A or B), |AΔB|.
🔎 You can click on the labels to view a diagram representing these sets and set relations.
- The Venn diagram calculator shall instantly calculate the cardinality of the remaining set relationships. It will also determine the size of the complements of these sets and set relations.
For example, consider a universal set with 50 elements, 20 of which are in set A and 20 in set B. Say 5 elements are common for both sets, and we want to know how many elements are exclusively in A or B.
In the Venn diagram calculator, first, select 2 sets and provide the cardinalities |U| = 50, |A| = 20, |B| = 20, and |A∩B| = 5. The calculator immediately gives us the cardinality of elements exclusively in A or in B, |AΔB| = 30. Additionally, it also provides the cardinalities of the remaining set relations and their complements:
- |A\B| = 15;
- |B\A| = 15;
- |A∪B| = 35;
- |A'| = 30;
- |B'| = 30;
- |(A\B)'| = 35;
- |(B\A)'| = 35;
- |(A∪B)'| = 15;
- |(A∩B)'| = 45; and
- |(AΔB)'| = 20.
The following article delves into sets, Venn diagrams, set relations, and set cardinalities. We recommend you read it to grasp a good understanding of these basics.
What are Venn diagrams? Introduction to set theory
A Venn diagram is a representation technique in set theory that allows you to visualize sets as closed curves, by convention either circles or ellipses. A set is a collection of elements: we are most interested in the cardinality (i.e., the number of elements or the size) of the sets, which is denoted as . When more than one set appears in a diagram, we can start defining relationships between them: there's the union, the intersection, and a whole list of set operations that only marginally resembles the ones we perform on numbers.
Let's jump to these operations and learn how to calculate a Venn diagram set's cardinality in the most basic example: two sets.
Venn diagram calculations for a 2 circle diagram
The first non-trivial Venn diagram involves two sets. You can see its most known representation in the picture below.

In this simple diagram, we can start identifying the various sets of interests:
-
The sets and .
-
The intersection between and : . This subset contains all the elements that belong both to and to .
-
The union of and : . The elements in this set belong to or .
-
The set differences: in this case we deal with elements that belong exclusively to (the subset ) or that belong exclusively to (the subset ).
-
The symmetric difference of the sets and . This set corresponds to the logical operation XOR, or "exclusive or" (visit the XOR calculator if you need a quick explanation of this operator). The set contains all the elements that belong to or to , but not to both.
🙋 For a quick refresh on unions and intersections, visit our union and intersection calculator.
Calculations in a 2-circle Venn diagram
Calculating the cardinality of the sets in a 2-circle Venn diagram is never too complex. However, the formulas of choice will depend greatly on the information you know about the problem. First and foremost, it lets you calculate the intersection from the union and vice-versa. In mathematical terms, this is the inclusion-exclusion principle:
Notice how we used the cardinality of the sets. The intersection's cardinality appears with a negative sign because we considered the intersection's elements twice while summing the cardinalities of and .
Once we know either the union or the intersection, we can calculate the set differences:
The symmetric difference is the sum of these two results, but we can also write it neatly:
3-set Venn diagram calculations
Let's increase the number of circles to 3. As you can see from the image below, the number of sets increases markedly.
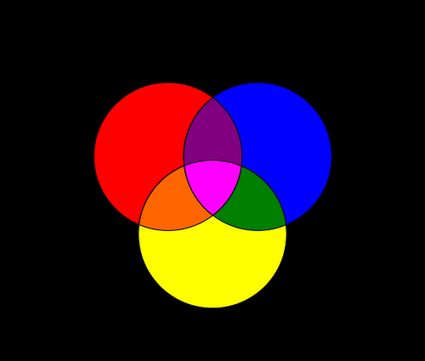
Now, for every pair of sets, we can define an intersection (, , ), and on top of them, an intersection between all their sets (). A similar approach applies to the union too.
To compute the union and intersection of the sets, we can use once again the inclusion-exclusion principle, but this time we will see it in a more complex form:
The sets in the second rows are the cardinalities of the intersections between each pair of sets: to calculate the union of , , and , you need to know those values, even though they are not of immediate importance.
In a 3-set Venn diagram, we calculate the difference between sets by knowing the value of the unions between each pair of sets or by carefully erasing the intersections from a set. In mathematical terms, this corresponds to these two formulas:
The first one uses unions of sets. The second one, which uses their intersections, requires a subtraction that erased the same set twice: in this case, we need to sum the 3-set intersection, too.
The last quantity we can calculate is the symmetric difference. In this instance, we will use a property of this operation: associativity:
This means we can calculate it first for two sets (something we know how to do), then consider the symmetric difference between the result and the third set. The result is an interesting figure:
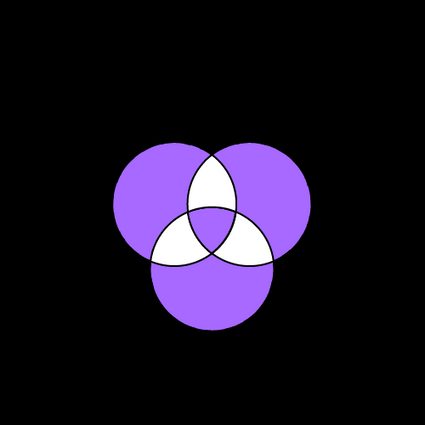
In this image, you can also see how the symmetric difference corresponds to the modulo 2 addition of the sets. Discover how to perform this operation at Omni's modulo calculator.
Increased complexity: some calculations for the 4 circle Venn diagram
Add one set. Now we are dealing with the four-set Venn diagram. To build a representation of it, we need to move away from circles: ellipses help create a diagram where each set appears once and only once.

Here we can identify 15 different sets: four set differences, six double intersections, four triple intersections, and one quadruple intersection. The complexity grows quickly enough that calculations can be performed only knowing a vast amount of data (14 out of the 15 sets, for example). In mathematical terms, we say that the number of sets grows with the binomial coefficient.
The situation is even more dramatic for a 5-set Venn diagram. In this case, we will only leave a representation of the symmetric difference here. Each of the purple-colored elements in this set must be computed individually. There are 16 subsets that together contribute to form this interesting, flower-like shape.

Enter the universe
For each of the quantities we listed above, we can define a complement. The complement of a set, in set theory, is the set that adds a "not" to the definition of the set it refers to. The complement of the intersection of and is the set that does not contain any element shared by both and . To define a complement, we need to define what's outside of our set.
In mathematical language, the set of everything we are not interested in is the universe, and we can represent it with a large set that encompasses our Venn diagram. In terms of notations, wrap your set in brackets (if needed) and add an apostrophe at the end. In the picture below, you can see the complement of the symmetric difference of three setsand the corresponding notation:
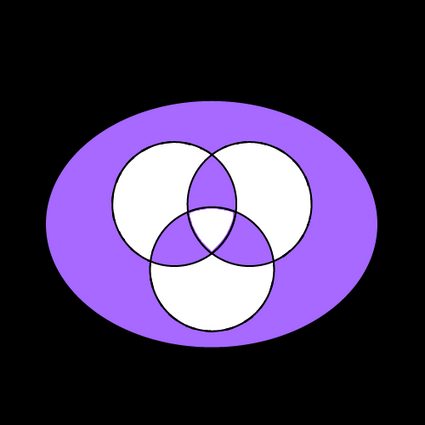
💡 Maybe, while reading this article, you noticed some similarities with another field of science: probability. Visit our probability calculator for 3 events to discover where set theory and probability theory meet.
Meet the creator of Venn diagram calculator
I'm Davide, a physicist experienced in creating math, physics, and engineering scientific tools. This calculator is part of my endeavor to help people solve complex-sounding problems with relative ease. Given the importance of data science and analysis in different areas, I wrote this companion article in the hopes of helping everyone understand set relations with the aid of Venn diagrams.
We take extra care to ensure the quality of our content so that it is as accurate and reliable as possible. Each tool is peer-reviewed by a trained expert and then proofread by a native speaker. To learn more about our standards, please check our Editorial Policies page.
FAQs
What is the inclusion-exclusion principle?
The inclusion-exclusion principle is a fundament of set theory, a formula that allows you to calculate the union or intersection of any number of sets. To calculate the union, follow these easy steps:
- Sum the cardinalities of the individual sets.
- Subtract the cardinality of the intersections of each pair of sets.
- Sum the cardinality of each intersection of three sets.
This alternate fashion of sum and difference repeats until you end up with possible intersections. This operation results in the cardinality of the union of the sets.
How do I calculate the intersection between three sets?
To calculate the intersection between three sets, A, B, and C, you can use the inclusion-exclusion principle. We assume you will know all the quantities mentioned.
- Find the cardinality of the union of all three sets (
|A ∪ B ∪ C|). - Subtract the cardinality of every single set(
|A|,|B|, and|C|). - Add the cardinality of the intersection of each pair of set (
|A ∩ B|,|A ∩ C|, and|B ∩ C|).
The result will be the cardinality of the intersection |A ∩ B ∩ C|.
What is the union if |A| = 10, |B| = 12, and |A ∩ B| = 4?
The union of A and B, with |A| = 10 and |B| = 12 is |A ∪ B| = 18. To find this result, we use the inclusion-exclusion principle:
- Calculate the sum of the cardinalities
|A|and|B|:|A| + |B| = 10 + 12 = 22. - Subtract the cardinality of their intersection:
|A| + |B| - |A ∩ B| = 22 - 4 = 18.
That's it. We subtracted the intersection because, by summing |A| and |B|, we inadvertently counted twice the elements shared by the two sets.
What is the symmetric difference of two sets?
The symmetric difference of two sets, A and B, is the set that contains all the elements belonging exclusively to either A or B. The corresponding logical operation is the exclusive or: when both sets exist in a given portion of the diagram, we disregard it. With higher numbers of sets in your diagram, use sum modulo 2 of the overlaps of the sets. If the overlaps are even, exclude the subset. If the overlaps are odd, include the subset.