Standard Deviation of Sample Mean Calculator

Calculating the standard deviation of the sample mean (aka standard deviation of the sampling distribution of the mean) is an excellent way to make sense of how the sample size influences the error of our estimates.

When the standard deviation of the mean is multiplied by a critical value, like the z-score or t-statistic, we obtain a margin of error that allows stating a confidence interval of our prediction. Therefore, calculating the standard deviation of the sampling distribution of the mean indicates where the population mean could be.

First of all, it's important to clarify that this term is known by various names such as:

• The standard deviation of the mean;
• The standard deviation of the sample mean;
• The standard deviation of the distribution of sample means; and
• The standard deviation of the sampling distribution of the sample mean.

It's also essential to know some definitions and concepts:

• Statistic: a point estimate or numeric characteristic of a sample (i.e., sample mean). It's different from a parameter, such as the population mean.
• Sampling distribution: the probability distribution of a randomly sampled statistic. In other words, it is the distribution of all the possible values that a statistic could take using the same sample size.
• Sampling distribution of the mean: this is an extension of the previous concept. If you have a population, take infinite samples of n size, and plot their means in a histogram, you get a probability distribution. That probability distribution is what we call the sampling distribution of the mean, and like any other distribution, it has its own mean and standard deviation.

The following diagram shows how to generate a sampling distribution of the mean. In reality, we don't use only six samples but an almost infinite number (i.e., 100,000).

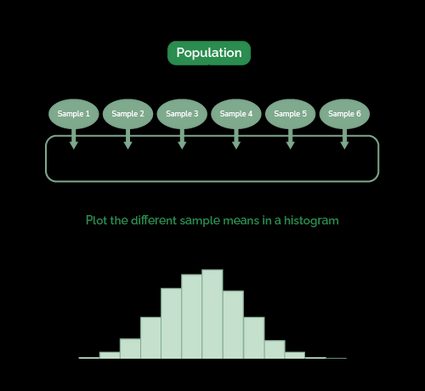
That said, we can define the standard deviation mean as the standard deviation of a distribution of means (like the one shown in the last diagram). Additionally, the mean of this sampling distribution is equal to the population mean.

Now that you know the concept, let's see how to calculate the standard deviation of the sample mean.

The difference between a sample and sampling distribution is:

• Sampling distribution: it's the term we usually hear. It refers to the probability distribution of a randomly sampled statistic. The sampling distribution of the mean is an example.
• Sample distribution: accounts for the distribution of the observations within only one sample. Each sample distribution possesses a mean, which helps form the sampling distribution.

The formula to find the standard deviation of the sample mean is:

σ_X̄ = σ/√n

where:

• σ_X̄ – Standard deviation of the sample mean;
• σ – Population standard deviation; and
• n - Sample size.

We previously said that if we know the mean of the sampling distribution (μ_X̄), we also know the population mean (μ), as they're equal (μ_X̄ = μ). In practice, we never know μ_X̄, but we can estimate it using the sample mean (X̄).

σ_X̄ indicates how X̄ approximates μ. The smaller σ_X̄, the nearest μ can be from our estimate. As σ is constant, increasing the sample size is the only way to diminish σ_X̄. Therefore, increasing n is a way to reduce our estimations' sampling error.

We know that the mean and standard deviation of the height of the adult American female population is about μ = 161.3 cm and σ = 7.1 cm. Now, suppose you randomly take samples of 100 women and take their mean height each time. What is the standard deviation of the sample mean?

To know the answer, follow these steps:

1. Input 7.1 in the population standard deviation box.
2. Input 100 in the sample size box.
3. That's it. The answer should be 0.71. Therefore, the standard deviation of the sampling distributions of means n = 100 is 0.71.

You can check the results using the formula: $σ_{\bar X} = \frac{σ}{\sqrt{n}} = \frac{7.1}{\sqrt{100}} = 0.71$