Last updated: Apr 23, 2024

OR Probability Calculator

Q: What is the probability of obtaining 1 OR 6 in two die tosses?

0.306 or ~31% . To find this result, follow these easy steps: Define the probability of obtaining 1 : P(1) = 1/6 = 0.167 . Define the probability of getting 6 : P(6) = 1/6 = 0.167 . Define the probability of obtaining 1 AND 6 : P(1 AND 6) = 1/6 × 1/6 = 1/36 = 0.028 . Calculate the probability of getting 1 OR 6 : P(1 OR 6) = P(1) + P(6) - P(1 AND 6) = 0.167 + 0.167 - 0.028 = 0.306 ≃ 31%

Q: How do I represent the OR probability in a Venn diagram?

In set theory, the OR probability corresponds to the union of the considered set . If you consider two not mutually exclusive events, you can identify four regions in your representation: The area outside the sets (no events happening); The area of the first event alone; The region of the second event alone; and The intersection between the two events. The OR probability encompasses all the regions that are not "no-events" , hence the single events and the intersection between them.

Created by Davide Borchia

Davide Borchia

Physicist by education, scientist by vocation. He holds a master’s degree in complex systems physics with a specialization in quantum technologies. If he is not reading something, he is outdoors trying to enjoy every bit of nature around him. He uses his memory as an advantage, and everything you will read from him contains at least one “I read about this five years ago” moment! See full profile

Check our editorial policy

Reviewed by Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

New

Table of contents

Before or, the probability of an event How do I find the probability of A OR B?How to calculate the OR probability Examples of applications of the OR probability formula Other probability calculators FAQs

Knowing how to calculate the OR probability is fundamental to probability theory. Omni will guide you with a simple yet exhaustive explanation of this basic concept.

Follow this article, and you will learn the following:

What is the probability of an event?
What is the OR probability of A and B?
How to find the probability of A or B?
Examples and detailed explanation.

Before or, the probability of an event

The probability of the outcome of an event corresponds to the fraction of times we may expect the particular outcome to happen out of the total amount of "happenings" of the event.

We can better grasp this concept with an example. Consider a die. Each outcome of a toss has probability $1/6 = 0.17$ (we call this uniform probability distribution, by the way: you can learn more about it at our uniform distribution calculator). We found this number since each number has $1$ probability out of $6$ to be the result of the toss, with $6$ the total amount of possible outcomes.

If the outcome of an event doesn't depend on any other event (or at least, not on the one we care for), we say that the event is independent. A fair coin toss is an excellent example of an independent event.

How do I find the probability of A OR B?

If you want to calculate the probability of two events happening singularly and not at the same time (or anyway, happening together at all), you need to calculate the probability of A or B.

Define the probabilities of the two events as $P(A)$ and $P(B)$ . Their values are the probability of the specified outcome. We calculate the probability that either one or the other happens with the following formula:

\scriptsize P(A\cup B) = P(A) +P(B) - P(A\cap B),

where we see the value of the joint probability of the events A and B, $P(A\cap B)$ .

What does this formula mean?

The first part is the sum of the probabilities of the two events. $P(A)+P(B)$ is the probability that we get the outcome A, both alone and together with the outcome B, summed to the probability to get B, in this case also alone and together with A.
The second part is the — relatively restricted — situation in which both of the events happen. For example, two heads in two coin tosses. We considered this quantity two times in the previous point, so we need to subtract it once now.
Subtracting the two quantities leaves us with the probability of either one or the other happening and the probability that the two events happen together.

This formula is easy to understand when considering the Venn representation of our probabilities.

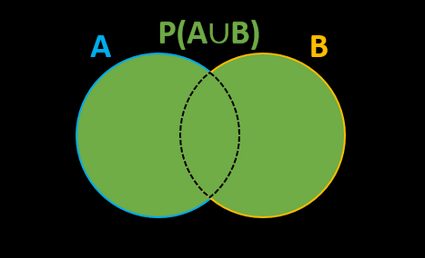
As you can see, the entire area representing the two events is colored green. The intersection is where the two events happen at once. The two remaining parts of the circle are the outcomes of the two events regardless of the other (obtaining head in one toss and tail in the other).

Notice that these calculations apply only for not mutually exclusive events. These are events that can't happen at the same time. Coin tosses come in our help again. The probability of obtaining heads OR tails in the same toss is an excellent example of mutually exclusive events. You can get either one or the other, but never both at the same time. In a Venn representation, the two sets would be disjointed.

If you are considering mutually exclusive events, the formula to calculate A OR B simplifies to:

P(A\cup B) + P(A)+P(B)

How to calculate the OR probability

In the formula for the OR probability, we meet the joint probability of the two events. We need to learn how to find this value if we want to be able to calculate the OR probability.

For independent events, the joint probability is the multiplication of the probability of the single events:

\scriptsize P(A\cap B)=P(A)\times P(B)

The formula for the OR probability is then:

\scriptsize \begin{split} P(A \cup B) &= P(A) +P(B) - P(A\cap B)\\ &= P(A)+P(B)-P(A)\times P(B) \end{split}

Examples of applications of the OR probability formula

You learned how to calculate the OR probability; it's time to test your knowledge with some examples.

Let's start with the basics. Use the OR probability formula to find the probability of obtaining at least one head in two coin tosses. You can directly apply the formula for the OR probability:

\scriptsize P(\mathrm{H}\cup \mathrm{H})\! =\! P(\mathrm{H})\!+\!P(\mathrm{H})\! -\! P(\mathrm{H}\cap \mathrm{H})

The three quantities on the right-hand side are, respectively:

The probability of obtaining a head in the first toss;
The probability of a head in the second toss; and
The probability of a head in both tosses.

Let's apply the formula for the probability of A OR B:

\scriptsize \begin{split} P(\mathrm{H}\cup \mathrm{H}) &= P(\mathrm{H})\!+\!P(\mathrm{H}) \!-\! P(\mathrm{H})\times P(\mathrm{H})\\ &=0.5+0.5-(0.5\times0.5) = 0.75\\ &=75\% \end{split}

It means that in three tosses out of four, you would get at least one time a head.

Other probability calculators

Probabilities are part of our daily lives. Calculating them, however, can be a bit on the tricky side. Omni has a vast assortment of tools for your needs, including:

The probability calculator; and
The AND probability calculator.

FAQs

How do I calculate the probability of the event A or the event B?

Assuming the events not to be mutually exclusive, the probability of the event A OR the event B is:

P(A ∪ B) = P(A) + P(B) + P(A ∩ B),

where:

P(A ∪ B) — The probability of either events; and
P(A ∩ B) — The probability of the event A AND the event B.

This last quantity is equal to:

P(A ∩ B) = P(A) × P(B),

for independent events.

What is the probability of obtaining 1 OR 6 in two die tosses?

0.306 or ~31%. To find this result, follow these easy steps:

Define the probability of obtaining 1:

P(1) = 1/6 = 0.167.
Define the probability of getting 6:

P(6) = 1/6 = 0.167.
Define the probability of obtaining 1 AND 6:

P(1 AND 6) = 1/6 × 1/6 = 1/36 = 0.028.
Calculate the probability of getting 1 OR 6:

P(1 OR 6) = P(1) + P(6) - P(1 AND 6) = 0.167 + 0.167 - 0.028 = 0.306 ≃ 31%

How do I calculate the OR probability of two mutually exclusive events?

Two events are mutually exclusive if they can't happen simultaneously. Think of getting tail and head during the same coin toss.

In this situation, the probability of the event A OR the event B is:

P(A OR B) = P(A) + P(B)

Think of the coin toss again: since P(H) = 0.5 and P(T) = 0.5, the probability of getting a tail or head is:

P(T OR H) = P(T) + P(H) = 0.5 + 0.5 = 1 = 100%

How do I represent the OR probability in a Venn diagram?

In set theory, the OR probability corresponds to the union of the considered set.

If you consider two not mutually exclusive events, you can identify four regions in your representation:

The area outside the sets (no events happening);
The area of the first event alone;
The region of the second event alone; and
The intersection between the two events.

The OR probability encompasses all the regions that are not "no-events", hence the single events and the intersection between them.

Related calculators

Sum of Squares Calculator Midrange Calculator Coefficient of Variation Calculator